题目内容
 如图,点P在函数y=
如图,点P在函数y=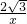 (x>0)的图象上运动,O为坐标原点,点A为PO的中点,以点P为圆心,PA为半径作⊙P,当⊙P与坐标轴相切时,则点P的坐标为________.
(x>0)的图象上运动,O为坐标原点,点A为PO的中点,以点P为圆心,PA为半径作⊙P,当⊙P与坐标轴相切时,则点P的坐标为________.
( ,
, ),(
),( ,
, )
)
分析:设点P(a,b),当圆P与x轴相切时,切点为C,根据点A为PO的中点,∠PEO=90°,可得a2+b2=4b2,由点P在函数y=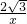 (x>0)的图象上,得ab=2
(x>0)的图象上,得ab=2 ,求出a和b的值,同理求出圆P与y轴相切时,同理可得P点坐标.
,求出a和b的值,同理求出圆P与y轴相切时,同理可得P点坐标.
解答:设点P(a,b),
当圆P与x轴相切时,切点为C,
∵点A为PO的中点,∠PEO=90°,
∴OP=2PE,
∴a2+b2=4b2,
∵点P在函数y=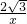 (x>0)的图象上,
(x>0)的图象上,
∴ab=2 ,
,
解得a= ,b=
,b= ,
,
此时P点坐标为( ,
, ),
),
当圆P与y轴相切时,同理可得P点坐标为( ,
, ),
),
综上所述,满足条件的P点坐标为( ,
, ),(
),( ,
, ),
),
故答案为( ,
, ),(
),( ,
, ).
).
点评:本题主要考查反比例函数的综合题,解答本题的关键是熟练掌握反比例函数的性质,解答此题需要分类讨论,此题难度不大,但是容易出现错误,希望同学们解答的时候注意.
 ,
, ),(
),( ,
, )
)分析:设点P(a,b),当圆P与x轴相切时,切点为C,根据点A为PO的中点,∠PEO=90°,可得a2+b2=4b2,由点P在函数y=
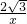 (x>0)的图象上,得ab=2
(x>0)的图象上,得ab=2 ,求出a和b的值,同理求出圆P与y轴相切时,同理可得P点坐标.
,求出a和b的值,同理求出圆P与y轴相切时,同理可得P点坐标.解答:设点P(a,b),
当圆P与x轴相切时,切点为C,
∵点A为PO的中点,∠PEO=90°,
∴OP=2PE,
∴a2+b2=4b2,
∵点P在函数y=
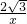 (x>0)的图象上,
(x>0)的图象上,∴ab=2
 ,
,解得a=
 ,b=
,b= ,
,此时P点坐标为(
 ,
, ),
),当圆P与y轴相切时,同理可得P点坐标为(
 ,
, ),
),综上所述,满足条件的P点坐标为(
 ,
, ),(
),( ,
, ),
),故答案为(
 ,
, ),(
),( ,
, ).
).点评:本题主要考查反比例函数的综合题,解答本题的关键是熟练掌握反比例函数的性质,解答此题需要分类讨论,此题难度不大,但是容易出现错误,希望同学们解答的时候注意.

练习册系列答案
相关题目
 如图,点A在函数
如图,点A在函数 如图,点A在函数
如图,点A在函数 如图,点A在函数y=
如图,点A在函数y= (2012•白下区二模)如图,点A在函数y=x(x≥0)图象上,且OA=
(2012•白下区二模)如图,点A在函数y=x(x≥0)图象上,且OA= 如图,点A在函数y=
如图,点A在函数y=