题目内容
今年国庆期间,县城某交巡警平台旁边的一个路口处,警察对某一段时间内来往车辆的车速情况进行了统计,并制成了如下两幅不完整的统计图:
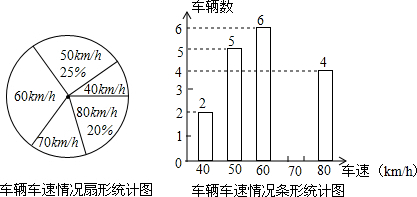
(1)这些车辆行驶速度的平均数是 千米/时,中位数是 千米/时.
(2)将条统计图补充完整.
(3)该路口限速60千米/时.经交警逐一排查,在超速的车辆中,车速为80千米/时的车辆中有2位驾驶员饮酒,车速为70千米/时的车辆中有1位驾驶员饮酒.若交警不是逐一排查,而是分别在车速为80千米/时和70千米/时的车辆中各随机拦下一位驾驶员询问,请你用列表法或画树状图的方法求出所选两辆车的驾驶员均饮酒的概率.

(1)这些车辆行驶速度的平均数是
(2)将条统计图补充完整.
(3)该路口限速60千米/时.经交警逐一排查,在超速的车辆中,车速为80千米/时的车辆中有2位驾驶员饮酒,车速为70千米/时的车辆中有1位驾驶员饮酒.若交警不是逐一排查,而是分别在车速为80千米/时和70千米/时的车辆中各随机拦下一位驾驶员询问,请你用列表法或画树状图的方法求出所选两辆车的驾驶员均饮酒的概率.
考点:条形统计图,扇形统计图,列表法与树状图法
专题:
分析:(1)根据平均数的求法,求出车辆速度的总和再除以辆数可求出平均数,根据中位数的定义可知,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
(2)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率.
(2)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率.
解答:解:(1)5÷25%=20辆,车速为70千米/时的车辆有20-2-5-6-4=3辆.
平均数为(40×2+50×5+60×6+70×3+80×4)÷20=61km/h.
第10辆与第11辆速度均为60km/h,故中位数为60km/h.
(2)将条统计图补充如下:

(3)列表得:
车速为70千米/时的车辆有3辆,车速为80千米/时的车辆有4辆,
所有出现的情况如下:共有12种等可能的结果,两辆车的驾驶员均饮酒的可能有两种,
故概率为
=
.
故答案为:61,60.
平均数为(40×2+50×5+60×6+70×3+80×4)÷20=61km/h.
第10辆与第11辆速度均为60km/h,故中位数为60km/h.
(2)将条统计图补充如下:

(3)列表得:
| 70酒 | 70 | 70 | |
| 80酒 | 是 | 否 | 否 |
| 80酒 | 是 | 否 | 否 |
| 80 | 否 | 否 | 否 |
| 80 | 否 | 否 | 否 |
所有出现的情况如下:共有12种等可能的结果,两辆车的驾驶员均饮酒的可能有两种,
故概率为
| 2 |
| 12 |
| 1 |
| 6 |
故答案为:61,60.
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
下列关于方程x2=1的结论正确的是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、只有一个实数根 |
| D、没有实数根 |
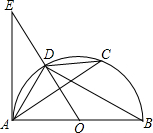 如图,已知AB是半⊙O的直径,过O作弦AC的垂线交半⊙O于D,交切线AE于E,连接BD、CD.
如图,已知AB是半⊙O的直径,过O作弦AC的垂线交半⊙O于D,交切线AE于E,连接BD、CD.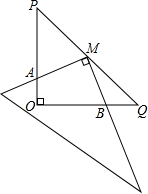 如图,在Rt△POQ中,OP=OQ,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB.
如图,在Rt△POQ中,OP=OQ,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB.