题目内容
19．
如图，若AB∥CD，则∠α=150°，∠β=80°，则∠γ=（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 30° |
分析 过点E作EF∥AB，根据平行线的性质可求出∠AEF的度数，进而得出∠CEF的度数，由此可得出结论．
解答 
解：过点E作EF∥AB，
∵∠α=150°，
∴∠AEF=180°-∠α=180°-150°=30°．
∵∠β=80°，
∴∠CEF=∠β-∠AEF=80°-30°=50°．
∵AB∥CD，EF∥AB，
∴EF∥CD，
∴∠γ=∠CEF=50°．
故选B．
点评 本题考查的是平行线的性质，根据题意作出辅助线是解答此题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
9．
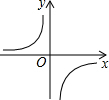已知函数$y=\frac{m}{x}$图象如图，以下结论，其中正确有（ ）个：
①m＜0；
②在每个分支上y随x的增大而增大；
③若A（-1，a），点B（2，b）在图象上，则a＜b
④若P（x，y）在图象上，则点P1（-x，-y）也在图象上．
已知函数$y=\frac{m}{x}$图象如图，以下结论，其中正确有（ ）个：①m＜0；
②在每个分支上y随x的增大而增大；
③若A（-1，a），点B（2，b）在图象上，则a＜b
④若P（x，y）在图象上，则点P1（-x，-y）也在图象上．
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
10．已知a=-（0.2）2，b=-22，c=（-$\frac{1}{2}$）-2，d=（-$\frac{1}{2}$）0，则比较a、b、c、d的大小结果是（ ）
| A． | a＜b＜c＜d | B． | a＜b＜d＜c | C． | b＜a＜d＜c | D． | b＜a＜c＜d |
如图：BC⊥AC，BC=8cm，AB=10cm，AC=6cm，那么点B到AC的距离为8cm．