题目内容
如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.
(1)试说明CE是⊙O的切线;
(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;
(3)设点D是线段AC上任意一点(不含端点),连接OD,当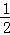 CD+OD的最小值为6时,求⊙O的直径AB的长.
CD+OD的最小值为6时,求⊙O的直径AB的长.
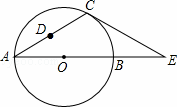
解:(1)连接OC,如图1,
∵CA=CE,∠CAE=30°,
∴∠E=∠CAE=30°,∠COE=2∠A=60°,
∴∠OCE=90°,
∴CE是⊙O的切线;
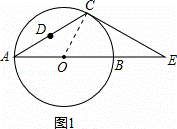
(2)过点C作CH⊥AB于H,连接OC,如图2,
由题可得CH=h.
在Rt△OHC中,CH=OC•sin∠COH,
∴h=OC•sin60°=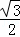 OC,
OC,
∴OC= =
=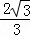 h,
h,
∴AB=2OC=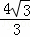 h;
h;
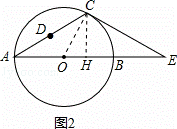
(3)作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,如图3,
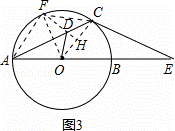
则∠AOF=∠COF=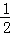 ∠AOC=
∠AOC=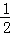 (180°﹣60°)=60°.
(180°﹣60°)=60°.
∵OA=OF=OC,
∴△AOF、△COF是等边三角形,
∴AF=AO=OC=FC,
∴四边形AOCF是菱形,
∴根据对称性可得DF=DO.
过点D作DH⊥OC于H,
∵OA=OC,∴∠OCA=∠OAC=30°,
∴DH=DC•sin∠DCH=DC•sin30°=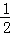 DC,
DC,
∴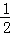 CD+OD=DH+F
CD+OD=DH+F D.
D.
根据两点之间线段最短可得:
当F、D、H三点共线时,DH+FD(即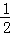 CD+OD)最小,
CD+OD)最小,
此时FH=OF•sin∠FOH=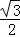 OF=6,
OF=6,
则OF=4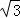 ,AB=2OF=8
,AB=2OF=8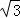 .
.
∴当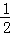 CD+OD的最小值为6时,⊙O的直径AB的长为8
CD+OD的最小值为6时,⊙O的直径AB的长为8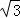 .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
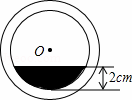
补充习题江苏系列答案将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
|
| A. | ( | B. | ( | C. | ( | D. | ( |
一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 |
| 13元 |
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
如图是某校参加各兴趣小组的学生人数分布扇形统计图,则参加人数最多的兴趣小组是( )

|
| A. | 棋类 | B. | 书画 | C. | 球类 | D. | 演艺 |
方程2x﹣1=3的解是( )
|
| A. | ﹣1 | B. | ﹣2 | C. | 1 | D. | 2 |
 π﹣4
π﹣4 )cm2
)cm2 π﹣4
π﹣4 )cm2
)cm2 π﹣2
π﹣2 9元
9元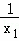 +
+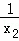 =3,则k的值是
=3,则k的值是 
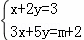 的解满足x+y=0,求实数m的值.
的解满足x+y=0,求实数m的值.