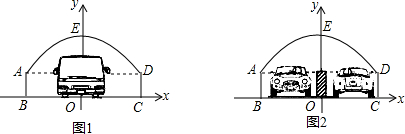题目内容
 已知,如图,正六边形ABCDEF的边长为6cm,求这个正六边形的外接圆半径R、边心距r6、面积S6.
已知,如图,正六边形ABCDEF的边长为6cm,求这个正六边形的外接圆半径R、边心距r6、面积S6.考点:正多边形和圆
专题:
分析:连接OA,OB,过点O作OG⊥AB于G,易得△AOB是等边三角形,继而可得正六边形的外接圆半径R,然后由勾股定理求得边心距,又由S正六边形=6S△ABC求得答案.
解答:解:连接OA,OB,过点O作OG⊥AB于G,
∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴OA=OB=6,即R=6,
∵OA=OB=6,OG⊥AB,
∴AG=
AB=
×6=3,
∴在Rt△AOG中,r6=OG=
=3
cm,
∴S6=
×6×6×3
=54
cm2.
∵∠AOB=60°,OA=OB,

∴△AOB是等边三角形,
∴OA=OB=6,即R=6,
∵OA=OB=6,OG⊥AB,
∴AG=
| 1 |
| 2 |
| 1 |
| 2 |
∴在Rt△AOG中,r6=OG=
| OA2-AG2 |
| 3 |
∴S6=
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题考查了正六边形的性质、等边三角形的判定与性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
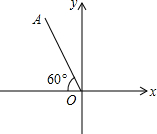 如图,OA=2,OA与x轴负半轴的夹角是60°,点A关于y轴的对称点是点A′,点P是x轴上一动点,当PA+PA′的值最小时,点P的坐标是( )
如图,OA=2,OA与x轴负半轴的夹角是60°,点A关于y轴的对称点是点A′,点P是x轴上一动点,当PA+PA′的值最小时,点P的坐标是( )| A、(-1,0) | ||
| B、(1,0) | ||
| C、(0,0) | ||
D、(
|
 有理数a、b在数轴上的位置如图所示,则a-b的值在( )
有理数a、b在数轴上的位置如图所示,则a-b的值在( )| A、-3与-2之间 |
| B、2与3之间 |
| C、0与1之间 |
| D、-2与-1之间 |
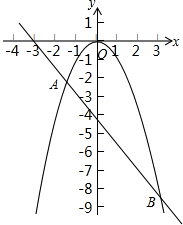 如图所示,抛物线y1=-x2与直线y2=-
如图所示,抛物线y1=-x2与直线y2=-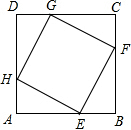 如图,在正方形ABCD中,E,F,G,H分别是边AB,BC,CD,DA上的点,且AE=BF=CG=DH,试判定四边形EFGH的形状,并证明你的结论.
如图,在正方形ABCD中,E,F,G,H分别是边AB,BC,CD,DA上的点,且AE=BF=CG=DH,试判定四边形EFGH的形状,并证明你的结论.