题目内容
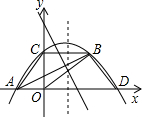
（1）已知如图1，△ABC和△ADE中，AB=AC，AD=AE，且∠CAB=∠DAE，连接CE、BD，求证：CE=BD；
（2）将△ADE绕着A点旋转，当点C、E、D在一条直线时如图2，上述结论是否成立？
（3）旋转到图3时，上述结论成立吗？
（4）旋转到图4时，此时点B、E、D在一条直线上，上述结论成立吗？若成立，请就（2）（3）（4）中的一种情况加以说明．
证明：（1）∵∠CAB=∠DAE，
∴∠CAB-∠BAE=∠DAE-∠BAE．
即∠CAE=∠BAD．
在△ACE和△ABD中
，
∴△ACE≌△ABD（SAS）．
∴CE=BD．
（2）、（3）、（4）结论成立．
分析：（1）求证CE=BD，应证明△ACE≌△ABD，根据SAS即可证明；
（2）、（3）、（4）的证明方法和（1）类似．
点评：证两条线段相等，通常是证这两条线段所在的两个三角形全等，类似的题，证明方法基本不变．
∴∠CAB-∠BAE=∠DAE-∠BAE．
即∠CAE=∠BAD．
在△ACE和△ABD中
，∴△ACE≌△ABD（SAS）．
∴CE=BD．
（2）、（3）、（4）结论成立．
分析：（1）求证CE=BD，应证明△ACE≌△ABD，根据SAS即可证明；
（2）、（3）、（4）的证明方法和（1）类似．
点评：证两条线段相等，通常是证这两条线段所在的两个三角形全等，类似的题，证明方法基本不变．
练习册系列答案
相关题目
过△ABC的三个顶点，已知如图，点C是线段AB的黄金分割点（AC＞BC），则下列结论中正确的是（ ）
| A、AB2=AC2+BC2 | ||||||
| B、BC2=AC•BA | ||||||
C、
| ||||||
D、
|
（2012•通州区一模）已知如图，在△ABC中，AB=AC，∠ABC=α，将△ABC以点B为中心，沿逆时针方向旋转α度（0°＜α＜90°），得到△BDE，点B、A、E恰好在同一条直线上，连接CE．
已知如图，菱形ABCD中，∠ADC=120°，BD=2