Question

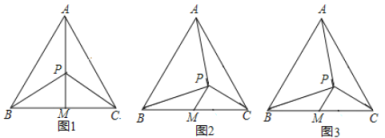
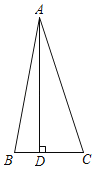
【题目】在△ABC中，∠BAC＝30°，AD⊥BC于D，BD＝4，CD＝6，则AD的长为_____．

Answer 1

【答案】

【解析】

作△ABC的外接圆⊙O，过O点作OE⊥BC于E，OF⊥AD于F，连接OB、OA、OC．则四边形OEDF为矩形，OA=OB=OC．易证△OBC为等边三角形，则OB=OC=BC=BD+CD=4+6=10，所以OA=OB=OC=10．再由勾股定理求出OE的长，即为DF的长，在Rt△AOF中，由勾股定理得，求出AF．最后由AD=AF+DF，求出AD的长．

作△ABC的外接圆⊙O，过O点作OE⊥BC于E，OF⊥AD于F，连接

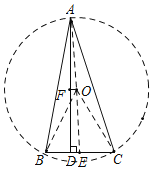
OB、OA、OC．
则四边形OEDF为矩形，OA=OB=OC．
∵∠BAC=30°，
∴∠BOC=2∠BAC=60°，
∴△OBC为等边三角形，
∴OB=OC=BC=BD+CD=4+6=10
∴OA=OB=OC=10．
∵OE⊥BC，
∴BE=CE=BC=5，
OE=，
DE=BE-BD=5-4=1，
∴OF=DE=1，DF=OE=5，
在Rt△AOF中，由勾股定理得，
AF= ，
∴AD=AF+DF=，
故答案为：．