题目内容
15．（1）解方程：$\frac{1}{x-2}$=$\frac{1-x}{2-x}$-3；（2）解不等式组：$\left\{\begin{array}{l}x-2＞0\\ 2（{x+1}）≥3x-1.\end{array}\right.$．
分析 （1）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解；
（2）分别求出不等式组中两不等式的解集，找出解集的公共部分即可．
解答 解：（1）去分母得：1=x-1-3x+6，
解得：x=2，
经检验x=2是增根，分式方程无解；
（2）$\left\{\begin{array}{l}{x-2＞0①}\\{2（x+1）≥3x-1②}\end{array}\right.$，
由①得：x＞2，
由②得：x≤3，
则不等式组的解集为2＜x≤3．
点评 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
5．P1（x1，y1），P2（x2，y2）是正比例函数y=$\frac{1}{3}$x图象上的两点，下列判断中，正确的是（ ）
| A． | y1＞y2 | B． | y1＜y2 | ||
| C． | 当x1＜x2 时，y1＜y2 | D． | 当x1＜x2 时，y1＞y2 |
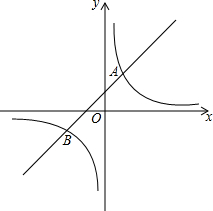如图，已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A（1，-k+4），B（n，-1）．
实数a，b在数轴上的位置如图所示，化简：$\sqrt{{a}^{2}-2ab+{b}^{2}}$-$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-|b-a|