ĢāÄæÄŚČŻ
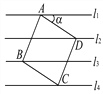
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy£½x2£«mx£«n¾¹żµćA(3£¬0)”¢
B(0£¬£3)£¬µćPŹĒÖ±ĻßABÉĻµÄ¶Æµć£¬¹żµćP×÷xÖįµÄ“¹Ļß½»Å×ĪļĻßÓŚµćM£¬ÉčµćPµÄŗį
×ų±źĪŖt£®
(1)·Ö±šĒó³öÖ±ĻßABŗĶÕāĢõÅ×ĪļĻߵĽāĪöŹ½£®
(2)ČōµćPŌŚµŚĖÄĻóĻŽ£¬Į¬½ÓAM”¢BM£¬µ±Ļ߶ĪPM×ī³¤Ź±£¬Ēó”÷ABMµÄĆ껿£®
(3)ŹĒ·ń“ęŌŚÕāŃłµÄµćP£¬Ź¹µĆŅŌµćP”¢M”¢B”¢OĪŖ¶„µćµÄĖıߊĪĪŖĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćPµÄŗį×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ½ā£ŗ(1)°ŃA£Ø3£¬0£©B£Ø0£¬-3£©“śČė![]() £¬µĆ
£¬µĆ
![]() ½āµĆ
½āµĆ![]()
ĖłŅŌÅ×ĪļĻߵĽāĪöŹ½ŹĒ![]() .
.
ÉčÖ±ĻßABµÄ½āĪöŹ½ŹĒ![]() ,°ŃA£Ø3£¬0£©B£Ø0£¬
,°ŃA£Ø3£¬0£©B£Ø0£¬![]() £©“śČė
£©“śČė![]() ,µĆ
,µĆ
![]() ½āµĆ
½āµĆ![]()
ĖłŅŌÖ±ĻßABµÄ½āĪöŹ½ŹĒ![]() .
.
(2)ÉčµćPµÄ×ų±źŹĒ£Ø![]() £©,ŌņM£Ø
£©,ŌņM£Ø![]() ,
,![]() £©,ŅņĪŖ
£©,ŅņĪŖ![]() ŌŚµŚĖÄĻóĻŽ£¬ĖłŅŌPM=
ŌŚµŚĖÄĻóĻŽ£¬ĖłŅŌPM=![]() £¬µ±PM×ī³¤Ź±
£¬µ±PM×ī³¤Ź±![]() £¬“ĖŹ±
£¬“ĖŹ±![]()
![]() =
=![]() =
=![]() .
.
£Ø3£©Čō“ęŌŚ£¬ŌņæÉÄÜŹĒ£ŗ
¢ŁPŌŚµŚĖÄĻóĻŽ£ŗĘ½ŠŠĖıߊĪOBMP ,PM=OB=3£¬ PM×ī³¤Ź±![]() £¬ĖłŅŌ²»æÉÄÜ.
£¬ĖłŅŌ²»æÉÄÜ.
¢ŚPŌŚµŚŅ»ĻóĻŽĘ½ŠŠĖıߊĪOBPM£ŗ PM=OB=3£¬![]() £¬½āµĆ
£¬½āµĆ![]() £¬
£¬![]() £ØÉįČ„£©£¬ĖłŅŌPµćµÄŗį×ų±źŹĒ
£ØÉįČ„£©£¬ĖłŅŌPµćµÄŗį×ų±źŹĒ![]() .
.
¢ŪPŌŚµŚČżĻóĻŽĘ½ŠŠĖıߊĪOBPM£ŗPM=OB=3£¬![]() £¬½āµĆ
£¬½āµĆ![]() £ØÉįČ„£©£¬
£ØÉįČ„£©£¬
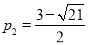 £¬ĖłŅŌPµćµÄŗį×ų±źŹĒ
£¬ĖłŅŌPµćµÄŗį×ų±źŹĒ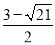 .
.
ĖłŅŌPµćµÄŗį×ų±źŹĒ![]() »ņ
»ņ![]() .
.
”¾½āĪö”æĀŌ

 Õć“óÓÅѧŠ”ѧğ¼¶ĻĪ½Óµ¼ÓėĮ·Õć½“óѧ³ö°ęÉēĻµĮŠ“š°ø
Õć“óÓÅѧŠ”ѧğ¼¶ĻĪ½Óµ¼ÓėĮ·Õć½“óѧ³ö°ęÉēĻµĮŠ“š°ø Š”ѧŹī¼Ł×÷Ņµ¶«ÄĻ“óѧ³ö°ęÉēĻµĮŠ“š°ø
Š”ѧŹī¼Ł×÷Ņµ¶«ÄĻ“óѧ³ö°ęÉēĻµĮŠ“š°ø ½ņĒŽĢÓżŹī¼Ł°ĪøßĻĪ½Ó¹ć¶«ČĖĆń³ö°ęÉēĻµĮŠ“š°ø
½ņĒŽĢÓżŹī¼Ł°ĪøßĻĪ½Ó¹ć¶«ČĖĆń³ö°ęÉēĻµĮŠ“š°ø ²Ø²ØŠÜŹī¼Ł×÷Ņµ½Ī÷ČĖĆń³ö°ęÉēĻµĮŠ“š°ø
²Ø²ØŠÜŹī¼Ł×÷Ņµ½Ī÷ČĖĆń³ö°ęÉēĻµĮŠ“š°ø”¾ĢāÄæ”æÅ×ĪļĻßy=©x2+bx+cÉĻ²æ·ÖµćµÄŗį×ų±źx£¬×Ż×ų±źyµÄ¶ŌÓ¦ÖµČēĻĀ±ķĖłŹ¾£ŗ
x | ” | ©2 | ©1 | 0 | 1 | 2 | ” |
y | ” | 0 | 4 | 6 | 6 | 4 | ” |
“ÓÉĻ±ķæÉÖŖ£¬ĻĀĮŠĖµ·ØÖŠ£¬“ķĪóµÄŹĒ£Ø””””£©
A. Å×ĪļĻßÓėxÖįµÄŅ»øö½»µć×ų±źĪŖ£Ø©2£¬0£© B. Å×ĪļĻßÓėyÖįµÄ½»µć×ų±źĪŖ£Ø0£¬6£©
C. Å×ĪļĻߵĶŌ³ĘÖįŹĒÖ±Ļßx=0 D. Å×ĪļĻßŌŚ¶Ō³ĘÖį×ó²ą²æ·ÖŹĒÉĻÉżµÄ