ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬¾ŲŠĪABCDµÄ±ßAB£½4£¬BC£½6£®Čō²»øıä¾ŲŠĪABCDµÄŠĪדŗĶ“󊔣¬µ±¾ŲŠĪ¶„µćAŌŚxÖįµÄÕż°ėÖįÉĻ×óÓŅŅĘ¶ÆŹ±£¬¾ŲŠĪµÄĮķŅ»øö¶„µćDŹ¼ÖÕŌŚyÖįµÄÕż°ėÖįÉĻĖęÖ®ÉĻĻĀŅĘ¶Æ£®
(1)µ±”ĻOAD£½30”揱£¬ĒóµćCµÄ×ų±ź£»
(2)ÉčADµÄÖŠµćĪŖM£¬Į¬½ÓOM”¢MC£¬µ±ĖıߊĪOMCDµÄĆ껿ĪŖ![]() Ź±£¬ĒóOAµÄ³¤£»
Ź±£¬ĒóOAµÄ³¤£»
(3)µ±µćAŅĘ¶Æµ½Ä³Ņ»Ī»ÖĆŹ±£¬µćCµ½µćOµÄ¾ąĄėÓŠ×ī“óÖµ£¬ĒėÖ±½ÓŠ“³ö×ī“óÖµ£¬²¢Ēó“ĖŹ±cos”ĻOADµÄÖµ£®

”¾“š°ø”æ(1)µćCµÄ×ų±źĪŖ(2£¬3+2![]() )£»(2)OA£½3
)£»(2)OA£½3![]() £»(3)OCµÄ×ī“óÖµĪŖ8£¬cos”ĻOAD£½
£»(3)OCµÄ×ī“óÖµĪŖ8£¬cos”ĻOAD£½![]() £®
£®
”¾½āĪö”æ
(1)×÷CE”ĶyÖį£¬ĻČÖ¤”ĻCDE£½”ĻOAD£½30”ćµĆCE£½![]() CD£½2£¬DE£½
CD£½2£¬DE£½![]() £¬ŌŁÓÉ”ĻOAD£½30”ćÖŖOD£½
£¬ŌŁÓÉ”ĻOAD£½30”ćÖŖOD£½![]() AD£½3£¬“Ó¶ųµĆ³öµćC×ų±ź£»
AD£½3£¬“Ó¶ųµĆ³öµćC×ų±ź£»
(2)ĻČĒó³öS”÷DCM£½6£¬½įŗĻSĖıߊĪOMCD£½![]() ÖŖS”÷ODM£½
ÖŖS”÷ODM£½![]() £¬S”÷OAD£½9£¬ÉčOA£½x”¢OD£½y£¬¾Ż“ĖÖŖx2+y2£½36£¬
£¬S”÷OAD£½9£¬ÉčOA£½x”¢OD£½y£¬¾Ż“ĖÖŖx2+y2£½36£¬![]() xy£½9£¬µĆ³öx2+y2£½2xy£¬¼“x£½y£¬“śČėx2+y2£½36ĒóµĆxµÄÖµ£¬“Ó¶ųµĆ³ö“š°ø£»
xy£½9£¬µĆ³öx2+y2£½2xy£¬¼“x£½y£¬“śČėx2+y2£½36ĒóµĆxµÄÖµ£¬“Ó¶ųµĆ³ö“š°ø£»
(3)ÓÉMĪŖADµÄÖŠµć£¬ÖŖOM£½3£¬CM£½5£¬ÓÉOC”ÜOM+CM£½8ÖŖµ±O”¢M”¢CČżµćŌŚĶ¬Ņ»Ö±Ļߏ±£¬OCÓŠ×ī“óÖµ8£¬Į¬½ÓOC£¬Ōņ“ĖŹ±OCÓėADµÄ½»µćĪŖM£¬ON”ĶAD£¬Ö¤”÷CMD”×”÷OMNµĆ![]() £¬¾Ż“ĖĒóµĆMN£½
£¬¾Ż“ĖĒóµĆMN£½![]() £¬ON£½
£¬ON£½![]() £¬AN£½AM©MN£½
£¬AN£½AM©MN£½![]() £¬ŌŁÓÉOA£½
£¬ŌŁÓÉOA£½![]() ¼°cos”ĻOAD£½
¼°cos”ĻOAD£½![]() æɵƓš°ø£®
æɵƓš°ø£®
(1)ČēĶ¼1£¬¹żµćC×÷CE”ĶyÖįÓŚµćE£¬
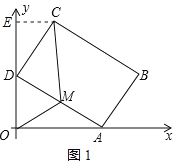
”ß¾ŲŠĪABCDÖŠ£¬CD”ĶAD£¬
”ą”ĻCDE+”ĻADO£½90”ć£¬
Ó֔ߔĻOAD+”ĻADO£½90”ć£¬
”ą”ĻCDE£½”ĻOAD£½30”ć£¬
”ąŌŚRt”÷CEDÖŠ£¬CE£½![]() CD£½2£¬DE£½
CD£½2£¬DE£½![]() £½2
£½2![]() £¬
£¬
ŌŚRt”÷OADÖŠ£¬”ĻOAD£½30”ć£¬
”ąOD£½![]() AD£½3£¬
AD£½3£¬
”ąµćCµÄ×ų±źĪŖ(2£¬3+2![]() )£»
)£»
(2)”ßMĪŖADµÄÖŠµć£¬
”ąDM£½3£¬S”÷DCM£½6£¬
ÓÖSĖıߊĪOMCD£½![]() £¬
£¬
”ąS”÷ODM£½![]() £¬
£¬
”ąS”÷OAD£½9£¬
ÉčOA£½x”¢OD£½y£¬Ōņx2+y2£½36£¬![]() xy£½9£¬
xy£½9£¬
”ąx2+y2£½2xy£¬¼“x£½y£¬
½«x£½y“śČėx2+y2£½36µĆx2£½18£¬
½āµĆx£½3![]() (øŗÖµÉįČ„)£¬
(øŗÖµÉįČ„)£¬
”ąOA£½3![]() £»
£»
(3)OCµÄ×ī“óÖµĪŖ8£¬
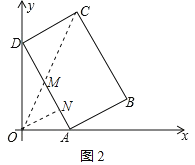
ČēĶ¼2£¬MĪŖADµÄÖŠµć£¬
”ąOM£½3£¬CM£½![]() £½5£¬
£½5£¬
”ąOC”ÜOM+CM£½8£¬
µ±O”¢M”¢CČżµćŌŚĶ¬Ņ»Ö±Ļߏ±£¬OCÓŠ×ī“óÖµ8£¬
Į¬½ÓOC£¬Ōņ“ĖŹ±OCÓėADµÄ½»µćĪŖM£¬¹żµćO×÷ON”ĶAD£¬“¹×ćĪŖN£¬
”ß”ĻCDM£½”ĻONM£½90”ć£¬”ĻCMD£½”ĻOMN£¬
”ą”÷CMD”×”÷OMN£¬
”ą![]() £¬¼“
£¬¼“![]() £¬
£¬
½āµĆMN£½![]() £¬ON£½
£¬ON£½![]() £¬
£¬
”ąAN£½AM©MN£½![]() £¬
£¬
ŌŚRt”÷OANÖŠ£¬OA£½![]() £¬
£¬
”ącos”ĻOAD£½![]() £®
£®