��Ŀ����
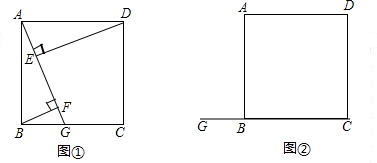
���ı���ABCD�У��Խ���AC��BD���ڵ�O����P�����߶�BC������һ�㣨���B���غϣ�����BPE=
��BCA��PE��BO�ڵ�E������B��BF��PE������ΪF����AC�ڵ�G��
��1����ABCD������
����ͼ��1��������P���C�غ�ʱ����BOG�Ƿ���ɡ�POEͨ��ij��ͼ�α任�õ���֤����Ľ��ۣ�
�ڽ��ͼ��2����
��ֵ��
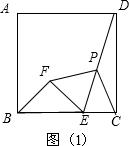
��2����ͼ��3������ABCDΪ���Σ��ǡ�BCA=������̽����ֱ��д��
��ֵ�����ú�����ʽ�ӱ�ʾ��

| 1 |
| 2 |
��1����ABCD������
����ͼ��1��������P���C�غ�ʱ����BOG�Ƿ���ɡ�POEͨ��ij��ͼ�α任�õ���֤����Ľ��ۣ�
�ڽ��ͼ��2����
| BF |
| PE |
��2����ͼ��3������ABCDΪ���Σ��ǡ�BCA=������̽����ֱ��д��
| BF |
| PE |

��1����BOG���ɡ�POE�Ƶ�O˳ʱ����ת90��õ���
֤������ͼ1�����ı���ABCD�������Σ�P��C�غϣ�
��OB=OP����BOC=��BOG=90�㣮
��PF��BG����PFB=90�㣬
���GBO=90��-��BGO��
��EPO=90��-��BGO��
���GBO=��EPO��
�ڡ�BOG�͡�POE��

���BOG�ա�POE��
��OE=OG��
�֡ߡ�EOG=90�㣬
�ཫ�߶�OE�Ƶ�O˳ʱ����ת90��͵õ�OG��
�֡�OB=OP����POB=90�㣬
�ཫ�߶�OP�Ƶ�O˳ʱ����ת90��͵õ�OB��
���BOG���ɡ�POE�Ƶ�O˳ʱ����ת90��õ���
��2����ͼ2����PM��AC��BG��M����BO��N��
���PNE=��BOC=90�㣬��BPN=��OCB��
�ߡ�OBC=��OCB=45�㣬���NBP=��NPB��
��NB=NP��
�ߡ�MBN=90��-��BMN����NPE=90��-��BMN��
���MBN=��NPE��
�ڡ�BMN�͡�PEN��
���BMN�ա�PEN��
��BM=PE��
�ߡ�BPE=
��ACB����BPN=��ACB��
���BPF=��MPF��
��PF��BM�����BFP=��MFP=90�㣮
�֡��ڡ�BPF�͡�MPF��
���BPF�ա�MPF��
��BF=MF����BF=
BM��
��BF=
PE����
=
��
��3����ͼ2����P��PM��AC��BG��M����BO��N��
���BPN=��BCA��
�ߡ�BPE=
��BCA��
���BPF=��MPF��
��PF��BG��
���BFP=��MFP��
�ڡ�BFP�͡�MFP��
���BFP�ա�MFP��ASA����
��BF=FM��
��BF=
BM��
���ı���ABCD�����Σ�
��DB��AC��
��PM��AC��
���BPN=��ACB=������PNE=��BOC=90�㣬
���BNM=90��
�ߡ�PFM=90�㣬
���MBN+��BMN=90�㣬��MPF+��BMN=90�㣬
���MBN=��NPE��
�ߡ�BNM=��ENP��
���BMN����PEN��
��
=
��
��tan��=
=
=
��
��
=
tan����

֤������ͼ1�����ı���ABCD�������Σ�P��C�غϣ�
��OB=OP����BOC=��BOG=90�㣮
��PF��BG����PFB=90�㣬
���GBO=90��-��BGO��
��EPO=90��-��BGO��
���GBO=��EPO��
�ڡ�BOG�͡�POE��
|

���BOG�ա�POE��
��OE=OG��
�֡ߡ�EOG=90�㣬
�ཫ�߶�OE�Ƶ�O˳ʱ����ת90��͵õ�OG��
�֡�OB=OP����POB=90�㣬
�ཫ�߶�OP�Ƶ�O˳ʱ����ת90��͵õ�OB��
���BOG���ɡ�POE�Ƶ�O˳ʱ����ת90��õ���
��2����ͼ2����PM��AC��BG��M����BO��N��
���PNE=��BOC=90�㣬��BPN=��OCB��
�ߡ�OBC=��OCB=45�㣬���NBP=��NPB��
��NB=NP��
�ߡ�MBN=90��-��BMN����NPE=90��-��BMN��
���MBN=��NPE��
�ڡ�BMN�͡�PEN��
|
���BMN�ա�PEN��
��BM=PE��
�ߡ�BPE=
| 1 |
| 2 |
���BPF=��MPF��
��PF��BM�����BFP=��MFP=90�㣮
�֡��ڡ�BPF�͡�MPF��
|
���BPF�ա�MPF��
��BF=MF����BF=
| 1 |
| 2 |
��BF=
| 1 |
| 2 |
| BF |
| PE |
| 1 |
| 2 |
��3����ͼ2����P��PM��AC��BG��M����BO��N��

���BPN=��BCA��
�ߡ�BPE=
| 1 |
| 2 |
���BPF=��MPF��
��PF��BG��
���BFP=��MFP��
�ڡ�BFP�͡�MFP��
|
���BFP�ա�MFP��ASA����
��BF=FM��
��BF=
| 1 |
| 2 |
���ı���ABCD�����Σ�
��DB��AC��
��PM��AC��
���BPN=��ACB=������PNE=��BOC=90�㣬
���BNM=90��
�ߡ�PFM=90�㣬
���MBN+��BMN=90�㣬��MPF+��BMN=90�㣬
���MBN=��NPE��
�ߡ�BNM=��ENP��
���BMN����PEN��
��
| BM |
| PE |
| BN |
| PN |
��tan��=
| BN |
| PN |
| BM |
| PE |
| 2BF |
| PE |
��
| BF |
| PE |
| 1 |
| 2 |


��ϰ��ϵ�д�
�����Ŀ