题目内容
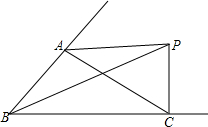 如图,P是△ABC中的∠BAC的外角平分线上一点.
如图,P是△ABC中的∠BAC的外角平分线上一点.(1)求证:PB+PC>AB+AC;
(2)若P是△ABC的∠BAC的平分线上一点且AC>AB,画出图形,试分析PB、PC、AB、AC间又有怎样的不等关系?
考点:全等三角形的判定与性质,三角形三边关系
专题:计算题
分析:(1)在BA延长线上截取AD=AC,连接DP,由AP平分∠DAC,得到一对角相等,利用SAS得到△ADP≌△ACP,利用全等三角形对应边相等得到PC=PD,在三角形BPD中,根据三边关系得到PB+PD>BD,等量代换即可得证;
(2)根据题意画出图形,在AC上截取AE=AB,连接PE,由AP平分∠BAC,得到一对角相等,利用SAS得到△ABP≌△AEP,利用全等三角形对应边相等得到BP=EP,在三角形PEC中,利用三角形三边关系得到PE+PC>EC,等量代换即可得证.
(2)根据题意画出图形,在AC上截取AE=AB,连接PE,由AP平分∠BAC,得到一对角相等,利用SAS得到△ABP≌△AEP,利用全等三角形对应边相等得到BP=EP,在三角形PEC中,利用三角形三边关系得到PE+PC>EC,等量代换即可得证.
解答: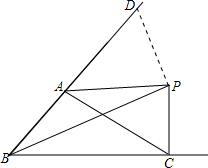 (1)证明:在BA延长线上截取AD=AC,连接DP,
(1)证明:在BA延长线上截取AD=AC,连接DP,
∵AP平分∠DAC,
∴∠DAP=∠CAP,
在△ADP和△ACP中,
,
∴△ADP≌△ACP(SAS),
∴PC=PD,
在△BPD中,PB+PD>BD=AB+AD,
∴PB+PC>AB+AC;
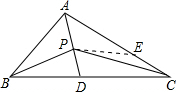 (2)解:如图所示:在AC上截取AE=AB,连接PE,
(2)解:如图所示:在AC上截取AE=AB,连接PE,
∵AP平分∠BAC,
∴∠BAP=∠EAP,
在△ABP和△AEP中,
,
∴△ABP≌△AEP(SAS),
∴BP=EP,
在△PEC中,PE+PC>EC,即PB+PC>EC=AC-AE=AC-AB.
 (1)证明:在BA延长线上截取AD=AC,连接DP,
(1)证明:在BA延长线上截取AD=AC,连接DP,∵AP平分∠DAC,
∴∠DAP=∠CAP,
在△ADP和△ACP中,
|
∴△ADP≌△ACP(SAS),
∴PC=PD,
在△BPD中,PB+PD>BD=AB+AD,
∴PB+PC>AB+AC;
 (2)解:如图所示:在AC上截取AE=AB,连接PE,
(2)解:如图所示:在AC上截取AE=AB,连接PE,∵AP平分∠BAC,
∴∠BAP=∠EAP,
在△ABP和△AEP中,
|
∴△ABP≌△AEP(SAS),
∴BP=EP,
在△PEC中,PE+PC>EC,即PB+PC>EC=AC-AE=AC-AB.
点评:此题考查了全等三角形的判定与性质,三角形的三边关系,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
方程2-4x=0的解是( )
A、x=
| ||
B、x=-
| ||
| C、x=2 | ||
| D、x=-2 |
| (x-3)2 |
| A、x<3 | B、x≤3 |
| C、x>3 | D、x≥3 |
已知y=kx+b,当x=0时,y=2;当x=2时,y=0,则当x=-2时,y等于( )
| A、-2 | B、0 | C、2 | D、4 |

