题目内容
在直角坐标系中,O为坐标原点,点A的坐标是(1,1),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是
- A.(
 ,0)
,0) - B.(1,0)
- C.(-
 ,0)
,0) - D.(-1,0)
D
分析:利用等腰三角形的定义和性质,以及两点之间的距离公式做题.
解答:①若AP=OP,设P点坐标为(x,0),则有
(x-0)2=(x-1)2+(0-1)2,
∴x=1,即P点坐标是(1,0)
②OA=AP,设P点坐标为(x,0),则有
(1-0)2+(1-0)2=(x-1)2+(0-1)2,
∴x1=0(不合题意,舍去),x2=2,
∴P点坐标是(2,0).
③OA=OP,设P点坐标是(x,0),则有
(x-0)2=(1-0)2+(1-0)2,
∴x2=2,
∴x=± ,
,
∴P点坐标是( ,0)或(-
,0)或(- ,0)
,0)
∴P点坐标不会是D(-1,0).
故选D.
点评:有两边相等的三角形是等腰三角形,以及两点之间的距离公式L=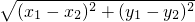 的利用.要分情况讨论.
的利用.要分情况讨论.
分析:利用等腰三角形的定义和性质,以及两点之间的距离公式做题.
解答:①若AP=OP,设P点坐标为(x,0),则有
(x-0)2=(x-1)2+(0-1)2,
∴x=1,即P点坐标是(1,0)
②OA=AP,设P点坐标为(x,0),则有
(1-0)2+(1-0)2=(x-1)2+(0-1)2,
∴x1=0(不合题意,舍去),x2=2,
∴P点坐标是(2,0).
③OA=OP,设P点坐标是(x,0),则有
(x-0)2=(1-0)2+(1-0)2,
∴x2=2,
∴x=±
 ,
,∴P点坐标是(
 ,0)或(-
,0)或(- ,0)
,0)∴P点坐标不会是D(-1,0).
故选D.
点评:有两边相等的三角形是等腰三角形,以及两点之间的距离公式L=
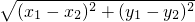 的利用.要分情况讨论.
的利用.要分情况讨论. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
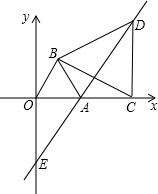 OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.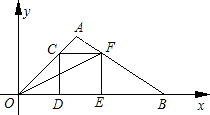 在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.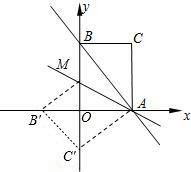 点B′处,C的对应点为C′.
点B′处,C的对应点为C′.