题目内容
14.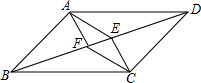 已知,如图,在?ABCD中,∠BAD和∠BCD的平分线AF,CE分别与对角线BD交于点F,E.求证:四边形AFCE是平行四边形.
已知,如图,在?ABCD中,∠BAD和∠BCD的平分线AF,CE分别与对角线BD交于点F,E.求证:四边形AFCE是平行四边形.
分析 利用平行四边形的性质得到AD=BC,AD∥BC,∠BAD=∠BCD,证明△DAF≌△BCE,得到AF=CE,∠AFD=∠CEB,从而得到AF∥CE,所以四边形AFCE是平行四边形.
解答 证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∠BAD=∠BCD,
∴∠ADB=∠CBD,
∵AF平分∠BAD,
∴∠DAF=$\frac{1}{2}$∠BAD,
∵CE平分∠BCD,
∴∠BCE=$\frac{1}{2}$∠BCD,
∴∠DAF=∠BCE,
在△DAF和△BCE中,
$\left\{\begin{array}{l}{∠ADB=∠CBD}\\{AD=BC}\\{∠DAF=∠BCE}\end{array}\right.$,
∴△DAF≌△BCE(ASA),
∴AF=CE,∠AFD=∠CEB,
∴AF∥CE,
∴四边形AFCE是平行四边形.
点评 本题考查了平行四边形的性质与判定,解决本题的关键是△DAF≌△BCE.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
9.下列图形中,旋转120°后能与原图形重合的是( )
| A. | 等边三角形 | B. | 正方形 | C. | 正五边形 | D. | 正八边形 |
4.为了维修某高速公路需开凿一条长为1300米的隧道,为了提高工作效率,高速公路建设指挥部决定由甲、乙两个工程队从两端同时开工.已知甲工程队比乙工程队每天能多开凿10米,且甲工程队开凿300米所用的天数与乙工程队开凿200米所用的天数相同,则甲、乙两个工程队每天各能开凿多少米( )
| A. | 甲20、乙30 | B. | 甲30、乙20 | C. | 甲40、乙30 | D. | 甲20、乙50 |
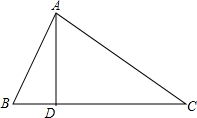 如图,三角形ABC中,AB=10,AC=17,AD与BC交于点D,AD=8,BD=6,求BC的长.
如图,三角形ABC中,AB=10,AC=17,AD与BC交于点D,AD=8,BD=6,求BC的长. 如图所示,AD∥BC,∠A=∠C,求∠AFB+∠CEA的度数.
如图所示,AD∥BC,∠A=∠C,求∠AFB+∠CEA的度数. △ABC中,∠B=30°,AB=8cm,BC=4cm,则△ABC的面积为8cm2.
△ABC中,∠B=30°,AB=8cm,BC=4cm,则△ABC的面积为8cm2.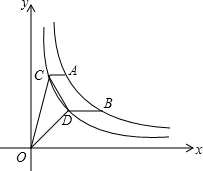 如图,点A、B在双曲线y1=$\frac{k}{x}$(k>1,x>0)上,点C、点D在双曲线y2=$\frac{1}{x}$(x>0)上,AC∥BD∥x轴,若$\frac{AC}{BD}$=m,则△OCD的面积为$\frac{1-{m}^{2}}{2m}$.(用含m的式子表示)
如图,点A、B在双曲线y1=$\frac{k}{x}$(k>1,x>0)上,点C、点D在双曲线y2=$\frac{1}{x}$(x>0)上,AC∥BD∥x轴,若$\frac{AC}{BD}$=m,则△OCD的面积为$\frac{1-{m}^{2}}{2m}$.(用含m的式子表示)
 如图,长方形的长为12,宽为x.
如图,长方形的长为12,宽为x.