题目内容
4.解下列不等式组,并将解集在数轴上表示出来.$\left\{\begin{array}{l}{\frac{x-1}{2}≤1}\\{x-2<4(x+1)}\end{array}\right.$.
分析 先分别解每个不等式,然后把解集表示在数轴上,确定公共部分.
解答 解:$\left\{\begin{array}{l}{\frac{x-1}{2}≤1①}\\{x-2<4(x+1)②}\end{array}\right.$
解不等式①得 x≤3;
解不等式②得 x>-2.
∴不等式组的解集为-2<x≤3.
把解集表示在数轴上为:
点评 此题考查了一元一次不等式组的解法,解不等式组既不能“代入”,也不能“加减”,而是要分别解不等式组中的每一个不等式,然后借助数轴找出解集的公共部分,从而得到不等式组的解集,熟练以后对于由两个不等式组成的不等式可按“同大取大,同小取小,大大小小无解,大小小大取中间”的规律间接地确定不等式组的解集.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
14. 如图,线段AB=4,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为( )
如图,线段AB=4,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为( )
 如图,线段AB=4,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为( )
如图,线段AB=4,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为( )| A. | 4 | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 2 |
13.如果m>n,ma与na比较,正确的是( )
| A. | ma>na | B. | ma=na | C. | ma<na | D. | 无法确定 |
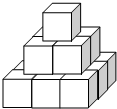 如图,几个棱长为1的小正方体在地板上堆积成一个模型,表面喷涂红色染料,那么染有红色染料的模型的表面积为42.
如图,几个棱长为1的小正方体在地板上堆积成一个模型,表面喷涂红色染料,那么染有红色染料的模型的表面积为42.