题目内容
12. 如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED=20°.
如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED=20°.
分析 由菱形的性质可知O为BD中点,所以OE为直角三角形BED斜边上的中线,由此可得OE=OB,根据等腰三角形的性质和已知条件即可求出∠OED的度数.
解答 解:
∵四边形ABCD是菱形,
∴DO=OB,
∵DE⊥BC于E,
∴OE为直角三角形BED斜边上的中线,
∴OE=$\frac{1}{2}$BD,
∴OB=OE,
∴∠OBE=∠OEB,
∵∠ABC=140°,
∴∠OBE=70°,
∴∠OED=90°-70°=20°,
故答案为:20°.
点评 本题考查了菱形的性质、直角三角形斜边上中线的性质,得到OE为直角三角形BED斜边上的中线是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
20. 如图所示的圆锥的主视图是( )
如图所示的圆锥的主视图是( )
 如图所示的圆锥的主视图是( )
如图所示的圆锥的主视图是( )| A. |  | B. |  | C. |  | D. |  |
17.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )


| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
14.化简$\frac{a}{a-b}$-$\frac{b}{a+b}$的结果是( )
| A. | $\frac{{a}^{2}{+b}^{2}}{{a}^{2}{-b}^{2}}$ | B. | $\frac{{(a+b)}^{2}}{{a}^{2}{-b}^{2}}$ | C. | $\frac{{a}^{2}{-b}^{2}}{{a}^{2}{+b}^{2}}$ | D. | $\frac{{a}^{2}{+b}^{2}}{{(a-b)}^{2}}$ |
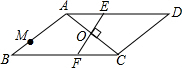 如图,在?ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为3:4.
如图,在?ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为3:4. 如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )
如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )



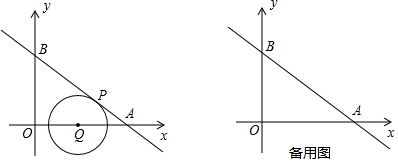
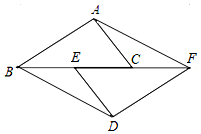 如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.
如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC. 如图所示,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=56°,∠E=32°,则∠F=36°.
如图所示,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=56°,∠E=32°,则∠F=36°.