题目内容
2.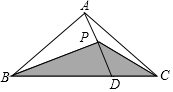 如图,在△ABC中,点D为BC边上一点,连接AD,取AD的中点P,连接BP,CP.若△ABC的面积为4cm2,则△BPC的面积为( )
如图,在△ABC中,点D为BC边上一点,连接AD,取AD的中点P,连接BP,CP.若△ABC的面积为4cm2,则△BPC的面积为( )| A. | 4cm2 | B. | 3cm2 | C. | 2cm2 | D. | 1cm2 |
分析 由点P为AD的中点,可得△ABP的面积=$\frac{1}{2}$S△ABD,S△CPD=$\frac{1}{2}$S△ACD,于是得到结论.
解答 解:∵点P是AD的中点,
∴△ABP的面积=$\frac{1}{2}$S△ABD,S△CPD=$\frac{1}{2}$S△ACD,
∴S△BPC=$\frac{1}{2}$S△ABC=2cm2,
故选C.
点评 本题考查了三角形的面积的计算,熟记等底等高的三角形的面积相等是解题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
10.下列线段能构成三角形的是( )
| A. | 3,3,5 | B. | 2,2,5 | C. | 1,2,3 | D. | 2,3,6 |
17.四舍五入得到的近似数0.70,下列说法正确的是( )
| A. | 精确到百位 | B. | 精确到十分位 | C. | 精确到百分位 | D. | 精确到千分位 |
7.画∠AOB的平分线的方法步骤是:
①以O为圆心,适当长为半径作弧,交OA于M点,交OB于N点;
②分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径作弧,两弧在∠AOB的内部相交于点C;
③过点C作射线OC.射线OC就是∠AOB的角平分线.
请你说明这样作角平分线的根据是( )
①以O为圆心,适当长为半径作弧,交OA于M点,交OB于N点;
②分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径作弧,两弧在∠AOB的内部相交于点C;
③过点C作射线OC.射线OC就是∠AOB的角平分线.
请你说明这样作角平分线的根据是( )
| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
14.若|a+1|+(b-2016)2=0,那么ab的值是( )
| A. | 1 | B. | -1 | C. | 2016 | D. | 1或-1 |
11.若a,b互为倒数,m,n互为相反数,则(m+n)2+2ab的值为( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
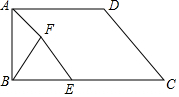 如图所示,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=7,BC=10,CD=6,E是BC边上一动点,以BE为一边在BC上方作等边△BEF,联结AF.
如图所示,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=7,BC=10,CD=6,E是BC边上一动点,以BE为一边在BC上方作等边△BEF,联结AF.