题目内容
 如图,DE与△ABC的边AB,AC分别相交于D,E两点,且DE∥BC.若DE=2cm,BC=3cm,EC=
如图,DE与△ABC的边AB,AC分别相交于D,E两点,且DE∥BC.若DE=2cm,BC=3cm,EC= cm,则AC等于
cm,则AC等于
- A.1
- B.

- C.

- D.2
D
分析:由DE∥BC可知,△ADE∽△ABC,根据相似三角形的性质,列出比例式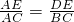 ,又知DE=2cm,BC=3cm,EC=
,又知DE=2cm,BC=3cm,EC= cm,可求出AE的长,从而求出AC的长.
cm,可求出AE的长,从而求出AC的长.
解答:∵DE∥BC,
∴△ADE∽△ABC,
∴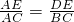 ,
,
即 ,
,
又∵DE=2cm,BC=3cm,EC= cm,
cm,
∴ ,
,
∴AE= ,
,
∴AC= +
+ =2.
=2.
故选D.
点评:本题考查了相似三角形的判定与性质,要找到相似三角形的对应边,并求出对应边的比.
分析:由DE∥BC可知,△ADE∽△ABC,根据相似三角形的性质,列出比例式
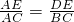 ,又知DE=2cm,BC=3cm,EC=
,又知DE=2cm,BC=3cm,EC= cm,可求出AE的长,从而求出AC的长.
cm,可求出AE的长,从而求出AC的长.解答:∵DE∥BC,
∴△ADE∽△ABC,
∴
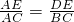 ,
,即
 ,
,又∵DE=2cm,BC=3cm,EC=
 cm,
cm,∴
 ,
,∴AE=
 ,
,∴AC=
 +
+ =2.
=2.故选D.
点评:本题考查了相似三角形的判定与性质,要找到相似三角形的对应边,并求出对应边的比.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 如图,DE与△ABC的边AB、AC分别相交于D、E两点,且DE∥BC.若DE=2cm,BC=3cm,EC=
如图,DE与△ABC的边AB、AC分别相交于D、E两点,且DE∥BC.若DE=2cm,BC=3cm,EC= 如图,DE与△ABC的边AB,AC分别相交于D,E两点,且DE∥BC.若DE=2cm,BC=3cm,EC=
如图,DE与△ABC的边AB,AC分别相交于D,E两点,且DE∥BC.若DE=2cm,BC=3cm,EC= (2013•中山一模)如图,DE与△ABC的边AB,AC分别相交于D,E两点,且DE∥BC.若AD:BD=3:1,DE=6,则BC等于( )
(2013•中山一模)如图,DE与△ABC的边AB,AC分别相交于D,E两点,且DE∥BC.若AD:BD=3:1,DE=6,则BC等于( ) ㎝,则AC=________㎝.
㎝,则AC=________㎝.
 cm,则AC= cm.
cm,则AC= cm.