Question

【题目】如图，菱形ABCD中，对角线AC，BD相交于点O，AC=12cm，BD=16cm，动点N从点D出发，沿线段DB以2cm/s的速度向点B运动，同时动点M从点B出发，沿线段BA以1cm/s的速度向点A运动，当其中一个动点停止运动时另一个动点也随之停止，设运动时间为t（s）（t＞0），以点M为圆心，MB长为半径的⊙M与射线BA，线段BD分别交于点E，F，连接EN．
（1）求BF的长（用含有t的代数式表示），并求出t的取值范围；
（2）当t为何值时，线段EN与⊙M相切？
（3）若⊙M与线段EN只有一个公共点，求t的取值范围．

Answer 1

【答案】
（1）解：连接MF．

∵四边形ABCD是菱形，

∴AB=AD，AC⊥BD，OA=OC=6，OB=OD=8，

在Rt△AOB中，AB= =10，

∵MB=MF，AB=AD，

∴∠ABD=∠ADB=∠MFB，

∴MF∥AD，

∴ = ，

∴ = ，

∴BF= t（0＜t≤8）．

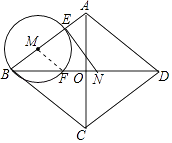
（2）解：当线段EN与⊙M相切时，易知△BEN∽△BOA，

∴ = ，

∴ = ，

∴t= ．

∴t= s时，线段EN与⊙M相切．

（3）解：①由题意可知：当0＜t≤ 时，⊙M与线段EN只有一个公共点．

②当F与N重合时，则有 t+2t=16，解得t= ，

关系图象可知， ＜t＜8时，⊙M与线段EN只有一个公共点．

综上所述，当0＜t≤ 或 ＜t＜8时，⊙M与线段EN只有一个公共点．

【解析】（1）连接MF．只要证明MF∥AD，可得 = ，即 = ，解方程即可；（2）当线段EN与⊙M相切时，易知△BEN∽△BOA，可得 = ，即 = ，解方程即可；（3）①由题意可知：当0＜t≤ 时，⊙M与线段EN只有一个公共点．②当F与N重合时，则有 t+2t=16，解得t= ，观察图象即可解决问题；