题目内容
18.已知二次函数y=x2+bx+5(b为常数),若在函数值y=1的情况下,只有一个自变量x的值与其对应,则此时b的值为±4.分析 根据在函数值y=l的情况下,只有一个自变量x的值与其对应,得到x2+bx+5=1有两个相等的实数根,求此时b的值即可.
解答 解:由题意得,x2+bx+5=1有两个相等的实数根,
所以△=b2-16=0,
解得,b=±4.
故答案为±4.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴是直线x=-$\frac{b}{2a}$,当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,因为图象有最低点,所以函数有最小值,当x=-$\frac{b}{2a}$时,y=$\frac{4ac-{b}^{2}}{4a}$;当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值,当x=-$\frac{b}{2a}$时,y=$\frac{4ac-{b}^{2}}{4a}$.

练习册系列答案
相关题目
13.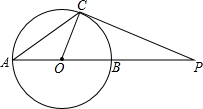 如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )
如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )
 如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )
如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )| A. | 40° | B. | 35° | C. | 30° | D. | 25° |
3.点P(-2,1)关于原点O对称的点的坐标是( )
| A. | (1,-2) | B. | (-1,2) | C. | (2,1) | D. | (2,-1) |
 如图,转盘中8个扇形的面积都相等,任意转动转盘1次.当转盘停止转动时,指针指向大于5的数的概率为$\frac{3}{8}$.
如图,转盘中8个扇形的面积都相等,任意转动转盘1次.当转盘停止转动时,指针指向大于5的数的概率为$\frac{3}{8}$.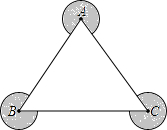 如图,△ABC是各边长都大于2的三角形,分别以它的顶点为圆心,1为半径画弧(弧的端点分别在三角形相邻两边上),则阴影部分的面积之和为$\frac{5}{2}$π.
如图,△ABC是各边长都大于2的三角形,分别以它的顶点为圆心,1为半径画弧(弧的端点分别在三角形相邻两边上),则阴影部分的面积之和为$\frac{5}{2}$π.