题目内容
5.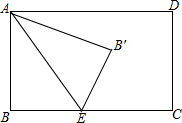 如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为( )
如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为( )| A. | 1或2 | B. | 2或3 | C. | 3或4 | D. | 4或5 |
分析 如图,连接B′D,过点B′作B′M⊥AD于M.设DM=B′M=x,则AM=7-x,根据等腰直角三角形的性质和折叠的性质得到:(7-x)2=25-x2,通过解方程求得x的值,易得点B′到BC的距离.
解答  解:如图,连接B′D,过点B′作B′M⊥AD于M.
解:如图,连接B′D,过点B′作B′M⊥AD于M.
∵点B的对应点B′落在∠ADC的角平分线上,
∴设DM=B′M=x,则AM=7-x,
又由折叠的性质知AB=AB′=5,
∴在直角△AMB′中,由勾股定理得到:AM2=AB′2-B′M2
即(7-x)2=25-x2,
解得x=3或x=4,
则点B′到BC的距离为2或1.
故选:A.
点评 本题考查了矩形的性质,翻折变换(折叠问题).解题的关键是作出辅助线,构建直角三角形△AMB′和等腰直角△B′DM,利用勾股定理将所求的线段与已知线段的数量关系联系起来.

练习册系列答案
相关题目
15.有40个数据,其中最大值为45,最小值为12,若取组距为5对数据进行分组,则应分为( )
| A. | 7组 | B. | 6组 | C. | 5组 | D. | 4组 |
20.若a>b,则下列不等式一定成立的是( )
| A. | a-b<0 | B. | $\frac{a}{3}$<$\frac{b}{3}$ | C. | -a>-b | D. | -a+1<-b+1 |
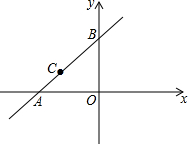 如图,直线y=x+4与坐标轴交于点A、B,点C(-3,m)在直线AB上,在y轴上找一点P,使PA+PC的值最小,求这个最小值及点P的坐标.
如图,直线y=x+4与坐标轴交于点A、B,点C(-3,m)在直线AB上,在y轴上找一点P,使PA+PC的值最小,求这个最小值及点P的坐标.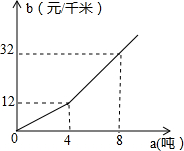 某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.
某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.
 如图,函数y1=ax+b与函数y2=cx+d相交于点A,点A的横坐标为1,若t=y1-y2,则令t>0的x的取值范围是x>1.
如图,函数y1=ax+b与函数y2=cx+d相交于点A,点A的横坐标为1,若t=y1-y2,则令t>0的x的取值范围是x>1. 如图,?DEFG内接于△ABC,已知△ADE、△EFC、△DBG的面积分别为1,2.8和1.2,则?DEFG的面积是4.
如图,?DEFG内接于△ABC,已知△ADE、△EFC、△DBG的面积分别为1,2.8和1.2,则?DEFG的面积是4.