题目内容

17．边数相同的两个正多边形的周长之比是$\sqrt{3}$：$\sqrt{2}$，则它们的面积比是3：2．

分析 根据相似多边形的周长之比求出相似比，根据相似多边形的面积之比等于相似比的平方计算即可．

解答 解：∵边数相同的两个正多边形的周长之比是$\sqrt{3}$：$\sqrt{2}$，
∴这两个正多边形的相似比比是$\sqrt{3}$：$\sqrt{2}$，
则这两个正多边形的面积之比是3：2，
故答案为：3：2．

点评 本题考查的是相似多边形的性质，掌握相似多边形对应边之比、周长之比等于相似比，而面积之比等于相似比的平方是解题的关键．

练习册系列答案
相关题目
7．已知：A=5a2-2b2-3c2，B=-3a2+b2+2c2，求2A-3（A+B）．
8．（-0.25）2000•（-4）2001=（　　）
A．4B．-4C．-1D．$\frac{1}{4}$
5．计算：
（1）-30-（-10）+（-8）
（2）-5.7+4.2+8-2.3-1$\frac{1}{5}$
（3）$\frac{2}{9}$-（-1$\frac{5}{6}$）+（-1$\frac{2}{9}$）-$\frac{1}{3}$
（4）（-8）×（-12）×（-12.5）×（-0.001）
（5）（$\frac{1}{2}$+$\frac{3}{4}$-$\frac{7}{6}$-$\frac{13}{12}$）×36
（6）-9$\frac{11}{20}$×0.375-9$\frac{11}{20}$×0.625
（7）-3.55-$\frac{1}{2}$（28.5-$\frac{2}{3}$）+（$\frac{2}{3}$-1.2）
12．“十一”期间，某商店举行促销活动，一种商品原价120元，按八折（即原价的80%）出售，则现售价应为96元．
2．已知（x+y+3）（x+y-3）=72，求x+y的值．
9．若-mxny是关于x，y的一个单项式，且其系数为3，次数为4，求mn的值．
6．先化简，再求值
（1）（2x2+x）-[4x2-2（3x2-x）]，其中x=-1$\frac{1}{2}$．
（2）4（$\frac{2m+3}{2}$-1）-3（$\frac{3-m}{3}$），其中m=$\frac{4}{5}$．
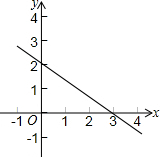7．如图，直线l是一次函数y=kx+b的图象，填空：
（1）当x=30时，y=-18；
（2）当y=30时，x=-42．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网