题目内容
 如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.(1)求证:AD平分∠BAC;
(2)求AC的长.
考点:切线的性质,相似三角形的判定与性质
专题:数形结合
分析:(1)首先连接OD,由BD是⊙O的切线,AC⊥BD,易证得OD∥AC,继而可证得AD平分∠BAC;
(2)由OD∥AC,易证得△BOD∽△BAC,然后由相似三角形的对应边成比例,求得AC的长.
(2)由OD∥AC,易证得△BOD∽△BAC,然后由相似三角形的对应边成比例,求得AC的长.
解答: (1)证明:连接OD,
(1)证明:连接OD,
∵BD是⊙O的切线,
∴OD⊥BD,
∵AC⊥BD,
∴OD∥AC,
∴∠2=∠3,
∵OA=OD,
∴∠1=∠3,
∴∠1=∠2,
即AD平分∠BAC;
(2)解:∵OD∥AC,
∴△BOD∽△BAC,
∴
=
,
∴
=
,
解得:AC=
.
 (1)证明:连接OD,
(1)证明:连接OD,∵BD是⊙O的切线,
∴OD⊥BD,
∵AC⊥BD,
∴OD∥AC,
∴∠2=∠3,
∵OA=OD,
∴∠1=∠3,
∴∠1=∠2,
即AD平分∠BAC;
(2)解:∵OD∥AC,
∴△BOD∽△BAC,
∴
| OD |
| AC |
| BO |
| BA |
∴
| 4 |
| AC |
| 6 |
| 10 |
解得:AC=
| 20 |
| 3 |
点评:此题考查了切线的性质以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
某事测得一周PM2.5的日均值(单位:)如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是( )
| A、50和50 |
| B、50和40 |
| C、40和50 |
| D、40和40 |
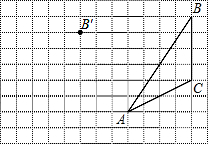 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.