题目内容
5.解方程组:(1)$\left\{\begin{array}{l}{\frac{x+y}{2}=\frac{2x-y}{3}}\\{\frac{x+y}{2}=x+2}\end{array}\right.$
(2)$\left\{\begin{array}{l}{2m+9n=4.8}\\{3m-5n=-15}\end{array}\right.$.
分析 (1)方程组整理后,利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)方程组整理得:$\left\{\begin{array}{l}{x=5y①}\\{x-y=-4②}\end{array}\right.$,
把①代入②得:5y-y=-4,即y=-1,
把y=-1代入①得:x=-5,
则方程组的解为$\left\{\begin{array}{l}{x=-5}\\{y=-1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2m+9n=4.8①}\\{3m-5n=-15②}\end{array}\right.$,
①×5+②×9得:37m=111,即m=3,
把m=3代入①得:n=$\frac{24}{5}$,
则方程组的解为$\left\{\begin{array}{l}{m=3}\\{n=\frac{24}{5}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
10.若关于x的方程$\frac{m}{x-4}$-$\frac{1-x}{4-x}$=0有增根,则增根是( )
| A. | -4 | B. | 1 | C. | 4 | D. | -1 |
17.计算($\sqrt{2}$)2的结果是( )
| A. | 4 | B. | ±2 | C. | -2 | D. | 2 |
14.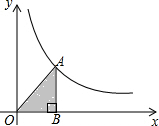 如图,在直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作AB⊥x轴于点B.当点A的横坐标逐渐增大时,△OAB的面积将会( )
如图,在直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作AB⊥x轴于点B.当点A的横坐标逐渐增大时,△OAB的面积将会( )
 如图,在直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作AB⊥x轴于点B.当点A的横坐标逐渐增大时,△OAB的面积将会( )
如图,在直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作AB⊥x轴于点B.当点A的横坐标逐渐增大时,△OAB的面积将会( )| A. | 逐渐增大 | B. | 不变 | C. | 先增大后减小 | D. | 逐渐减小 |