题目内容
18．已知抛物线y=x2+2bx-2，当-1≤x≤2时，y的最小值是$\left\{\begin{array}{l}{2+4b}&{b≤-2}\\{-{b}^{2}-2}&{-2＜b＜1}\\{-1-2b}&{b≥1}\end{array}\right.$．分析 根据题意可以利用分类讨论的数学思想求出y的最小值，本题得以解决．
解答 解：∵y=x2+2bx-2=（x+b）2-b2-2，
∴当-b≥2时，即b≤-2，则x=2时，y取得最小值，此时y=2+4b；
当-b≤-1时，即b≥1，则x=-1时，y去的最小值，此时y=-1-2b；
当-1＜-b＜2时，即-2＜b＜1，则x=-b时，y取得最小值，此时y=-b2-2；
由上可得，y的最小值是：$\left\{\begin{array}{l}{2+4b}&{b≤-2}\\{-{b}^{2}-2}&{-2＜b＜1}\\{-1-2b}&{b≥1}\end{array}\right.$，
故答案为：$\left\{\begin{array}{l}{2+4b}&{b≤-2}\\{-{b}^{2}-2}&{-2＜b＜1}\\{-1-2b}&{b≥1}\end{array}\right.$．
点评 本题考查二次函数的最值，解题的关键是明确题意，利用分类讨论的数学思想解答．
练习册系列答案
相关题目
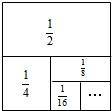利用图形来表示数量或数量关系，也可以利用数量或数量关系来描述图形特征或图形之间的关系，这种思想方法称为数形结合．我们刚学过的第9章《整式乘法与因式分解》就很好地体现了这一思想方法，你能利用数形结合的思想解决下列问题吗？