题目内容
11.经市场调查了解到,在“端午节”期间,甲、乙两种商品将会畅销,我市某商店决定去厂家选购这两种商品,若购进甲种商品7件,乙种商品2件,需要760元,若购进甲种商品5件,乙种商品4件,则需要800元.(1)求甲、乙两种商品每件进价分别是多少元?
(2)该商品经研究决定在“端午节”期间销售时吗,甲种商品的售价定为每件100元,乙种商品的售价定为每件125元,若该商店准备用不超过3440元的资金购进甲乙两种商品共40件,且这两种商品全部售出后总利润(利润=售价-进价)要超过850元,通过计算求出该商店有几种进货方案?请你设计出来.
分析 (1)设甲种商品每件进价是x元,乙种商品每件进价是y元,根据“购进甲种商品7件,乙种商品2件,需要760元,若购进甲种商品5件,乙种商品4件,则需要800元.”列出方程组解答即可;
(2)设购进甲种商品a件,则乙种商品40-a件,根据“不超过3440元的资金,全部售出后总利润(利润=售价-进价)要超过850元”列出不等式解答即可.
解答 解:(1)设甲种商品每件进价是x元,乙种商品每件进价是y元,由题意得
$\left\{\begin{array}{l}{7x+2y=760}\\{5x+4y=800}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=80}\\{y=100}\end{array}\right.$
答:甲种商品每件进价是80元,乙种商品每件进价是100元;
(2)设购进甲种商品a件,则乙种商品40-a件,由题意得
$\left\{\begin{array}{l}{80a+100(40-a)≤3440}\\{(100-80)a+(125-100)(40-a)>850}\end{array}\right.$,
解得:28≤a<30,
∵a是整数,
∴a=28或29,则40-a=12或11,
答:该商店有两种进货方案:购进甲种商品28件,乙种商品12件或购进甲种商品29件,乙种商品11件.
点评 此题主要考查了二元一次方程组的应用以及一元一次不等式的应用,解决本题的关键是读懂题意,找到所求量的等量关系及符合题意的不等关系式组.

练习册系列答案
相关题目
2.正比例函数y=6x的图象与反比例函数y=$\frac{4}{x}$的图象的交点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第一、三象限 |
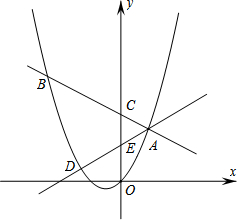 如图,抛物线y=x2+bx+c过原点O及点A(1,2),过点A的直线交抛物线于另一点B,交y轴于点C,过点A的另一条直线交抛物线于另一点D,交y轴于点E,且∠ACE=∠AEC.
如图,抛物线y=x2+bx+c过原点O及点A(1,2),过点A的直线交抛物线于另一点B,交y轴于点C,过点A的另一条直线交抛物线于另一点D,交y轴于点E,且∠ACE=∠AEC.