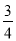题目内容
已知二次函数y=x2﹣2(k+1)x+k2﹣2k﹣3与x轴有两个交点.
(Ⅰ)求k取值范围;
(Ⅱ)当k取最小整数时,此二次函数的对称轴和顶点坐标;
(Ⅲ)将(Ⅱ)中求得的抛物线在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象.请你求出新图象与直线y=x+m有三个不同公共点时m的值.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
根据下表回答下列问题:
x | 16.0 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256.00 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 |
(1)265.69的平方根是 , 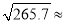 ;
;
(2)表中与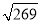 最接近的数是 .
最接近的数是 .


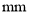 ),其中不合格的是( )
),其中不合格的是( )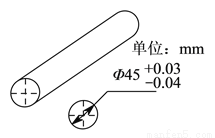
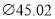 B.
B. 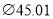 C.
C. 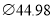 D.
D. 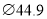
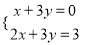 那么(
那么(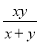 +2)÷
+2)÷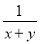 的值为___.
的值为___.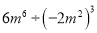 的结果为( )
的结果为( )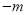 B. ﹣1 C.
B. ﹣1 C. 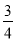 D. ﹣
D. ﹣