题目内容
 抛物线:y=ax2+2ax+a2+2的一部分如图所示,那么该抛物线在y轴右侧与x轴交点的坐标是________.
抛物线:y=ax2+2ax+a2+2的一部分如图所示,那么该抛物线在y轴右侧与x轴交点的坐标是________.
(1,0)
分析:先把点(-3,0)代入y=ax2+2ax+a2+2中求出a的值,得到完整的解析式后,再利用ax2+2ax+a2+2=0解出x的值,即求出对应的x值,可得到右侧交点坐标.
解答:由图可知点(-3,0)在抛物线上,
把(-3,0)代入y=ax2+2ax+a2+2中,得
9a-6a+a2+2=0,解得a=-1或a=-2;
当a=-1时,y=-x2-2x+3=-(x+3)(x-1),
设y=0,则x1=-3,x2=1,
∴在y轴右侧与x轴交点的坐标是(1,0);
当a=-2时,y=-2x2-4x+6=-2(x+3)(x-1),
设y=0,则x1=-3,x2=1,
∴在y轴右侧与x轴交点的坐标是(1,0).
∴抛物线在y轴右侧与x轴交点的坐标是(1,0).
点评:熟练掌握解方程和熟悉抛物线的性质.
分析:先把点(-3,0)代入y=ax2+2ax+a2+2中求出a的值,得到完整的解析式后,再利用ax2+2ax+a2+2=0解出x的值,即求出对应的x值,可得到右侧交点坐标.
解答:由图可知点(-3,0)在抛物线上,
把(-3,0)代入y=ax2+2ax+a2+2中,得
9a-6a+a2+2=0,解得a=-1或a=-2;
当a=-1时,y=-x2-2x+3=-(x+3)(x-1),
设y=0,则x1=-3,x2=1,
∴在y轴右侧与x轴交点的坐标是(1,0);
当a=-2时,y=-2x2-4x+6=-2(x+3)(x-1),
设y=0,则x1=-3,x2=1,
∴在y轴右侧与x轴交点的坐标是(1,0).
∴抛物线在y轴右侧与x轴交点的坐标是(1,0).
点评:熟练掌握解方程和熟悉抛物线的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 16、抛物线:y=ax2+2ax+a2+2的一部分如图所示,那么该抛物线在y轴右侧与x轴交点的坐标是
16、抛物线:y=ax2+2ax+a2+2的一部分如图所示,那么该抛物线在y轴右侧与x轴交点的坐标是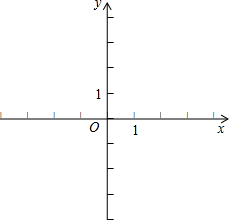 已知双曲线:
已知双曲线: 一个涵洞成抛物线形,它的截面如图.现测得,当水面宽AB=1.6m时,涵洞顶点O与水面的距离为2.4m.ED离水面的高FC=1.5m,求涵洞ED宽是多少?是否会超过1m?(提示:设涵洞所成抛物线为y=ax2(a<0))
一个涵洞成抛物线形,它的截面如图.现测得,当水面宽AB=1.6m时,涵洞顶点O与水面的距离为2.4m.ED离水面的高FC=1.5m,求涵洞ED宽是多少?是否会超过1m?(提示:设涵洞所成抛物线为y=ax2(a<0))