题目内容
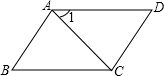 如图,已知∠1=30°,∠B=60°,AB⊥AC,
如图,已知∠1=30°,∠B=60°,AB⊥AC,
(1)∠DAB+∠B=________;
(2)AB与CD平行吗?为什么?AD与BC平行吗?为什么?
解:(1)∵AB⊥AC,
∴∠BAC=90°,
∵∠B=60°,∠1=30°
∴∠DAB+∠B=30°+90°+60°=180°,
故答案为:180°.
(2)答:AB与CD不平行,
理由是根据已知条件不能推出AB∥CD.
AD与BC平行,
理由是:∵AB⊥AC,
∴∠BAC=90°,
∵∠B=60°,∠1=30°,
∴∠DAB+∠B=30°+90°+60°=180°,
∴AD∥BC.
分析:(1)根据三角形的内角和定理求出∠ACB,根据平行线的判定证出AD∥BC即可;
(2)根据三角形的内角和定理求出∠ACB=∠1,根据平行线的判定即可推出答案.
点评:本题主要考查对平行线的性质和判定,三角形的内角和定理等知识点的理解和掌握,能推出∠ACB=∠1是解此题的关键.
∴∠BAC=90°,
∵∠B=60°,∠1=30°
∴∠DAB+∠B=30°+90°+60°=180°,
故答案为:180°.
(2)答:AB与CD不平行,
理由是根据已知条件不能推出AB∥CD.
AD与BC平行,
理由是:∵AB⊥AC,
∴∠BAC=90°,
∵∠B=60°,∠1=30°,
∴∠DAB+∠B=30°+90°+60°=180°,
∴AD∥BC.
分析:(1)根据三角形的内角和定理求出∠ACB,根据平行线的判定证出AD∥BC即可;
(2)根据三角形的内角和定理求出∠ACB=∠1,根据平行线的判定即可推出答案.
点评:本题主要考查对平行线的性质和判定,三角形的内角和定理等知识点的理解和掌握,能推出∠ACB=∠1是解此题的关键.

练习册系列答案
相关题目

 28、如图,已知∠AOB=30°,∠BOC=50°,∠COD=21°,OE平分∠AOD,求∠AOE的度数.(精确到分)
28、如图,已知∠AOB=30°,∠BOC=50°,∠COD=21°,OE平分∠AOD,求∠AOE的度数.(精确到分) 如图,已知∠1=30°,∠3=110°,那么∠2的度数为
如图,已知∠1=30°,∠3=110°,那么∠2的度数为 如图,已知∠AOB=30°,P为其内部一点,OP=3,M、N分别为OA、OB边上的一点,要使△PMN的周长最小,请给出确定点M、N位置的方法,并求出最小周长.
如图,已知∠AOB=30°,P为其内部一点,OP=3,M、N分别为OA、OB边上的一点,要使△PMN的周长最小,请给出确定点M、N位置的方法,并求出最小周长.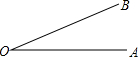 如图,已知∠AOB=30°.
如图,已知∠AOB=30°.