题目内容
9. 如图,AD是△ABC的∠A的平分线,若∠B=40°,∠C=60°,则∠ADB=100°.
如图,AD是△ABC的∠A的平分线,若∠B=40°,∠C=60°,则∠ADB=100°.
分析 根据三角形内角和定理求出∠BAC,根据角平分线定义请求出∠BAD,根据三角形内角和定理求出即可.
解答 解:∵∠B=40°,∠C=60°,
∴∠BAC=180°-∠B-∠C=80°,
∵AD是△ABC的∠A的平分线,
∴∠BAD=$\frac{1}{2}$∠CAB=40°,
∴∠ADB=180°-∠B-∠BAD=100°.
故答案为:100°.
点评 本题考查了三角形内角和定理的应用,能正确利用三角形内角和定理求出∠BAC的度数是解此题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
19.下列语句不是命题的是( )
| A. | 延长AB到D,使BD=$\frac{1}{3}$AB | B. | 两点之间线段最短 | ||
| C. | 两条直线相交有且只有一个交点 | D. | 等角的补角相等 |
17.以下说法正确的是( )
①一条直角边和斜边上的高对应相等的两个直角三角形全等;
②有两条边相等的两个直角三角形全等;
③有一边相等的两个等边三角形全等;
④两边和其中一边的对角对应相等的两个三角形全等.
①一条直角边和斜边上的高对应相等的两个直角三角形全等;
②有两条边相等的两个直角三角形全等;
③有一边相等的两个等边三角形全等;
④两边和其中一边的对角对应相等的两个三角形全等.
| A. | ①② | B. | ②④ | C. | ①③ | D. | ①③④ |
18.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:

(1)根据上面多面体的模型,完成表格中的空格:
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2;
(2)一个多面体的棱数比顶点数大10,且有12个面,则这个多面体的棱数是30;
(3)某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形两种多边形拼接而成,每个顶点处都有3条棱,共有棱36条.若该多面体外表面三角形的个数比八边形的个数的2倍多2,求该多面体外表面三角形的个数.

(1)根据上面多面体的模型,完成表格中的空格:
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
(2)一个多面体的棱数比顶点数大10,且有12个面,则这个多面体的棱数是30;
(3)某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形两种多边形拼接而成,每个顶点处都有3条棱,共有棱36条.若该多面体外表面三角形的个数比八边形的个数的2倍多2,求该多面体外表面三角形的个数.
 如图所示,并按要求作图:
如图所示,并按要求作图: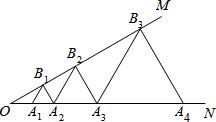 如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4 …均为等边三角形,若OA1=$\frac{1}{3}$,则△A2015B2015A2016的边长为$\frac{{2}^{2014}}{3}$.
如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4 …均为等边三角形,若OA1=$\frac{1}{3}$,则△A2015B2015A2016的边长为$\frac{{2}^{2014}}{3}$. 如图,AB=16cm,延长AB到C,使BC=3AB,D是BC的中点,求AD的长度.
如图,AB=16cm,延长AB到C,使BC=3AB,D是BC的中点,求AD的长度.