��Ŀ����
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ����յ�
����λ���ȵ��ٶ����յ�![]() �˶�������
�˶�������![]() ���
���![]() ��
��![]() ���غ�ʱ������
���غ�ʱ������![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ����
����![]() ��������������
��������������![]() ����������
����������![]() ��
��![]() �ص�����ͼ�ε����Ϊ
�ص�����ͼ�ε����Ϊ![]() ��ƽ����λ������
��ƽ����λ������![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() ���룩��
���룩��
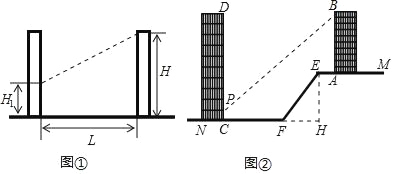
�������� ����ͼ
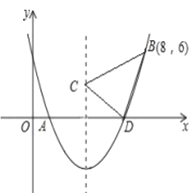
��1���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �ij���
�ij���
��2��ֱ��д����![]() ��
��![]() �ڲ�ʱ
�ڲ�ʱ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��4��ֱ��д����![]() ����
����![]() ����λ������ֱ����ʱ
����λ������ֱ����ʱ![]() ��ֵ��
��ֵ��
���𰸡���1��PQ=![]() ����2��
����2��![]() ����3����
����3����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ����4��
����4��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��������
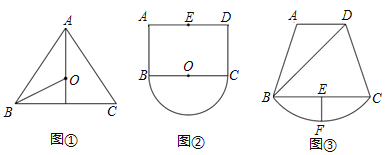
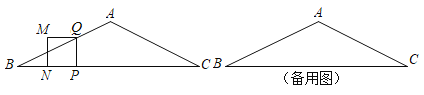
��1���������������:����Q���߶�AB��ʱ,����Q���߶�AC��ʱ;
��2���ȼ���M�ڱ�AB��ʱt��ֵ,���ݵ�M�ڡ�ABC�ڲ�ʱ�����߽�㼴�ɽ��;
��3�����������:
��0��t��1ʱ,������PQMN���ABC�ص�����ͼ�����ı���DNPQ,
����1��t��![]() ʱ,������PQMN���ABC�ص�����ͼ���������ODNPQ,
ʱ,������PQMN���ABC�ص�����ͼ���������ODNPQ,
����![]() ��t��2ʱ,������PQMN���ABC�ص�����ͼ����������MNPQ,
��t��2ʱ,������PQMN���ABC�ص�����ͼ����������MNPQ,
�ֱ�����������;
��4����M���ڡ�ABC����λ������ֱ����ʱ,�����������,��ͼ�ɽ��
��:��1���������:BP��2t,
��ͼ1,��A��AD��BC��D,
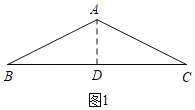
��AB��AC��![]() ,BC��4,
,BC��4,
��BD��CD��![]() BC��2��
BC��2��
��AD��![]() ,
,
��tan��B��![]() ��
��![]() ,
,
���������:
������Q���߶�AB��ʱ,��0��t��1ʱ,��ͼ2,
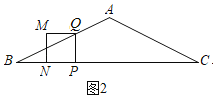
��tan��B��![]() ,
,
��PQ��t;
������Q���߶�AC��ʱ,��1��t��2ʱ,��ͼ3,
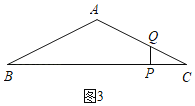
��tan��C��tan��B��![]() ��
��![]() ,
,
��PQ��![]() PC��
PC��![]() ��2��t;
��2��t;
��2����M�ڱ�AB��ʱ,��ͼ4,
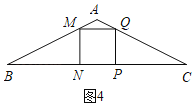
�ɣ�1��֪:MN��PQ��2��t��PN,
tan��B��![]() ��
��![]() ,
,
��BN��2MN,
��BP��BN+PN,
��2t��3MN��3��2��t��,
t��![]() ,
,
���M�ڡ�ABC�ڲ�ʱt��ȡֵ��Χ��![]() ��t��2;
��t��2;
��3�����������:
��0��t��1ʱ,��ͼ5,������PQMN���ABC�ص�����ͼ�����ı���DNPQ,
BP��2t,PQ��PN��MD��t,
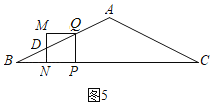
��BN��2t��t��t,
��DN��![]() t��DM,
t��DM,
��S��S������MNPQ��S��MDQ��![]() ;
;
����1��t��![]() ʱ,��ͼ6,������PQMN���ABC�ص�����ͼ���������ODNPQ,
ʱ,��ͼ6,������PQMN���ABC�ص�����ͼ���������ODNPQ,
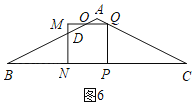
��PQ��PN��MN��2��t,
��BN��BP��PN��2t����2��t����3t��2,
��tan��B��![]() ,DN��
,DN��![]() BN��
BN��![]() ,
,
��DM��MN��DN��2��t��![]() ��3��
��3��![]() t,
t,
��tan��MOD��tan��B��![]() ��
��![]() ,
,
��OM��2MD,
��S��S������MNPQ��S��MDO����2��t��2��![]() ����2��t��2��
����2��t��2��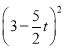 ����
����![]() +11t��5;
+11t��5;
����![]() ��t��2ʱ,��ͼ7,������PQMN���ABC�ص�����ͼ����������MNPQ,
��t��2ʱ,��ͼ7,������PQMN���ABC�ص�����ͼ����������MNPQ,
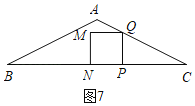
S��PQ2����2��t��2��t2��4t+4;
����,S��t֮��ĺ�����ϵʽΪ:S��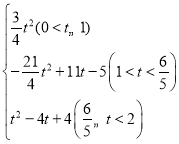 ��
��
��4�������������:
����ͼ8,M����λ��MQ��,��Q��AB���е�,BQ��![]() ,
,
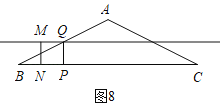
��BP��1��2t,
t��![]() ;
;
����ͼ9,M����λ��MT��,��T��BC���е�,BT��2,

��MT��AC,
���C����BTM,
��tan��BTM��![]() ,
,
��NT��BP,
��BP+TN��BT��PN,
��2t+2t��2��t,t��![]() ;
;
����ͼ10,M����λ��MQ��,
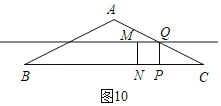
��Q��AC���е�,
ͬ����CP��1��4��2t,t��![]() ,
,
����ͼ11,M����λ��MT��,T��BC���е�,
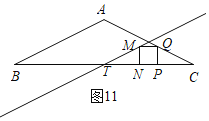
CP��TN��4��2t,PQ��PN��2��t,
��CT��TN+PN+PC,
��2��2��4��2t��+2��t,
t��![]() ;
;
����,t��ֵ��![]() ���
���![]() ���
���![]() ���
���![]() �룮
�룮