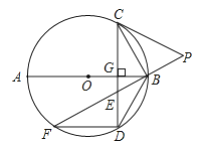
题目内容
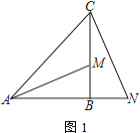
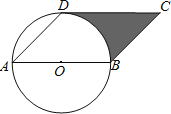
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于点
于点![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,延长
,延长![]() 至点
至点![]() ,连接
,连接![]() ,使
,使![]() ,延长
,延长![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,
,![]() .
.
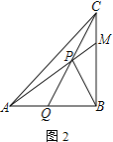
(1)连结![]() ,求证:
,求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线;
的切线;
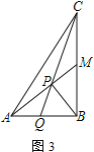
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据等边对等角可得∠CDB=∠FBD,然后根据同弧所对的圆周角相等可得∠BCD=∠F,最后利用AAS即可证出结论;
(2)连接OC,根据圆周角定理和三角形外角的性质证出∠COB=∠CEB,然后根据等边对等角、直角三角形的性质和等量代换即可求出∠OCP=90°,最后根据切线的判定定理即可证出结论;
(3)连接AC,先证出∠F=∠A=∠BCG,根据等角的正切值相等可得![]() ,设CG=2x,则AG=3x,BG=
,设CG=2x,则AG=3x,BG=![]() ,然后根据题意列出方程即可求出CG、AG、BG、AB,然后根据垂径定理求出DG,最后根据tan∠COB = tan∠CEB,即可求出结论.
,然后根据题意列出方程即可求出CG、AG、BG、AB,然后根据垂径定理求出DG,最后根据tan∠COB = tan∠CEB,即可求出结论.
解:(1)∵![]()
∴∠CDB=∠FBD
∵![]()
∴∠BCD=∠F
在△BCD和△DFB中
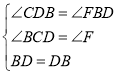
∴![]()
(2)连接OC
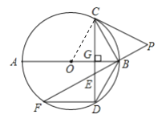
∵∠COB=2∠CDB,∠CEB=∠EDB+∠EBD=2∠EDB
∴∠COB=∠CEB
∵![]()
∴∠PCE=∠CEB
∴∠COB=∠PCE
∵![]()
∴∠OGC=90°
∴∠COB+∠OCG=90°
∴∠PCE+∠OCG=90°
∴∠OCP=90°
即OC⊥PC
∴![]() 是
是![]() 的切线;
的切线;
(3)连接AC
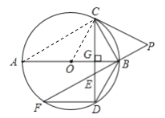
∴∠ACB=90°,
∴∠A+∠ACG=90°,∠BCG+∠ACG=90°
∴∠A=∠BCG
∵![]()
∴∠F=∠A=∠BCG
![]()
∴![]()
设CG=2x,则AG=3x,BG=![]()
∵![]()
∴![]()
∴CG=![]() ,AG=
,AG=![]() ,BG=
,BG=![]()
∴AB=AG+BG=![]() ,DG=CG=
,DG=CG=![]()
∴OB=![]() AB=
AB=![]()
∴OG=OB-BG=![]()
由(2)知∠COB=∠CEB
∴tan∠COB = tan∠CEB
∴![]()
即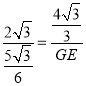
解得:GE=![]()
∴ED=DG-GE=![]()

 新编小学单元自测题系列答案
新编小学单元自测题系列答案【题目】某服装店同时购进甲、乙两种款式的运动服共![]() 套,进价和售价如表中所示,设购进甲款运动服
套,进价和售价如表中所示,设购进甲款运动服![]() 套(
套(![]() 为正整数),该服装店售完全部甲、乙两款运动服获得的总利润为
为正整数),该服装店售完全部甲、乙两款运动服获得的总利润为![]() 元.
元.
运动服款式 | 甲款 | 乙款 |
进价(元 |
|
|
售价(元 |
|
|
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)该服装店计划投入![]() 万元购进这两款运动服,则至少购进多少套甲款运动服?若售完全部的甲、乙两款运动服,则服装店可获得的最大利润是多少元?
万元购进这两款运动服,则至少购进多少套甲款运动服?若售完全部的甲、乙两款运动服,则服装店可获得的最大利润是多少元?
(3)在(2)的条件下,若服装店购进甲款运动服的进价降低![]() 元(其中
元(其中![]() ),且最多购进
),且最多购进![]() 套甲款运动服,若服装店保持这两款运动服的售价不变,请你设计出使该服装店获得最大销售利润的购进方案.
套甲款运动服,若服装店保持这两款运动服的售价不变,请你设计出使该服装店获得最大销售利润的购进方案.