题目内容
已知AD是△ABC的高，∠DAB=45°，∠DAC=30°，则∠BAC= °．
考点：三角形内角和定理
专题：分类讨论
分析：此题分情况讨论：①当高在△ABC内部；②当高在△ABC外部，分别对每一种情况画图，再结合图计算即可．
解答：解：①当高在△ABC内部，如右图
∵∠DAB=45°，∠DAC=30°，
∴∠BAC=45°+30°=75°；
②当高在△ABC外部，如右图
∵∠DAB=45°，∠DAC=30°，
∴∠BAC=45°-30°=15°．
故∠BAC=75°或15°．
故答案为：75或15．
∵∠DAB=45°，∠DAC=30°，
∴∠BAC=45°+30°=75°；
②当高在△ABC外部，如右图
∵∠DAB=45°，∠DAC=30°，
∴∠BAC=45°-30°=15°．
故∠BAC=75°或15°．
故答案为：75或15．
点评：本题考查了三角形内角和定理，解题的关键是注意分高在三角形内外两种情况讨论求解．
练习册系列答案
相关题目
下列各式从左到右的变形属于因式分解的是（ ）
| A、（M-2）（M-3）=（3-M）（2-M） |
| B、a2-2a+3=（a-1）2+2 |
| C、（x+1）（x-1）=x2-1 |
| D、1-a2=（1+a）（1-a） |
如图，△ABD≌△BAC，若∠C=95°，∠ABC=50°，则∠ABD=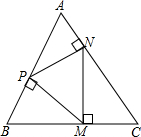
如图，点P、M、N分别在正△ABC的各边上，且MP⊥AB，MN⊥BC，PN⊥AC．求证：