题目内容

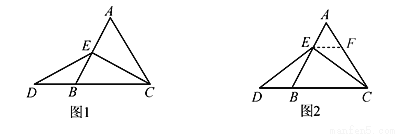
如图，在等边△ABC中，点E为边AB上任意一点，点D在边CB的延长线上，且ED＝EC．

（1）当点E为AB的中点时（如图1），则有AE DB（填“＞”“＜”或“＝”）；

（2）猜想AE与DB的数量关系，并证明你的猜想．

（1）=；（2）AE＝BD． 【解析】试题分析： （1）△BCE中可证，∠BCE=30°，又EB=EC，则∠D=∠ECB=30°，所以△BCE是等腰三角形，结合AE=BE即可； （2）过E作EF∥BC交AC于F，用AAS证明△DEB≌△ECF． 试题解析： （1）∵△ABC是等边三角形，∴∠ABC＝60°，AB＝AC＝BC. ∵E为AB的中点，所以∠BCE=30...
练习册系列答案
相关题目

若(m－2)x|m|－1＝5是一元一次方程，则m＝________．

-2 【解析】试题分析：因为（m-2）x|m|-1=5是一元一次方程，所以，又因为，所以．

下列方程中,一元二次方程的个数是：①x2-2x-1=0；②-x2=0；③ax2+bx+c=0；④ ；⑤；⑥.

A. 1个 B. 2个 C. 3个 D. 4个

B 【解析】试题解析：①②是一元二次方程. 故选B.

如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB，垂足为E．若PE=3，则两平行线AD与BC间的距离为（　　）

A. 3 B. 5 C. 6 D. 不能确定

C 【解析】试题解析：作PF⊥AD于F，PG⊥BC于G， ∵AP是∠BAD的角平分线，PF⊥AD，PE⊥AB， ∴PF=PE=3， ∵BP是∠ABC的角平分线，PE⊥AB，PG⊥BC， ∴PG=PE=3， ∵AD∥BC， ∴两平行线AD与BC间的距离为PF+PG=6， 故选C．

化简的结果为（　　）

A. B. C. D.

B 【解析】=,故选B.

已知，求＝___________．

． 【解析】试题解析：已知等式整理得： ，即 则原式 故答案为：

下列等式从左到右的变形，属于因式分解的是（ ）

A. a（x－y）＝ax－ay B. x2－1＝（x+1）（x－1）

C. （x+1）（x+3）＝x2+4x+3 D. x2+2x+1＝x（x+2）+1

B 【解析】试题分析：根据因式分解的定义只有B,是把一个多项式转化为两个因式积的形式.

已知，a－b=2，那么2a－2b+5=_________．

9 【解析】试题分析：把a－b=2代入得，2a－2b+5=2（a－b）+5=2×2-5=-1．

关于x的一元二次方程（m﹣1）x2+x+m2﹣1=0的一个根是0，则m的值是（ ）

A．﹣1 B．1 C．1或﹣1 D．﹣1或0

A 【解析】 试题分析：将x=0代入可得：-1=0，解得：m=1，根据方程的定义可得：m1，则m=-1.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网