题目内容
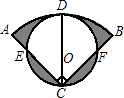如图，扇形CAB的圆心角∠ACB=90°，半径CA=8cm，D为弧AB的中点，以CD为直径的⊙O与CA、CB相交于点E、F，则弧AB的长为________cm，图中阴影部分的面积是________cm2．
4π （16π-32）
分析：连接EF，根据阴影部分的面积=扇形CAB的面积+圆O的面积-2（△CEF的面积+半圆的面积），即可求解．
解答：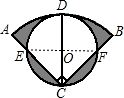
解：连接EF．
弧AB的长是：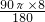
=4π（cm）；
扇形CAB的面积是：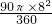
=16π（cm2）；
等腰直角△CEF的面积是
×8×4=16（cm2）；
以CD为直径的半圆的面积是：×（8÷2）2×π=8π（cm2）；
圆O的面积是16π（cm2）；
则16π+16π-2×（16+8π）=（16π-32）（cm2）．
故答案是：4π，（16π-32）．
点评：本题主要考查了扇形面积的计算，正确理解阴影部分的面积=扇形CAB的面积+圆O的面积-2（△CEF的面积+半圆的面积）是解题的关键．
分析：连接EF，根据阴影部分的面积=扇形CAB的面积+圆O的面积-2（△CEF的面积+半圆的面积），即可求解．
解答：
解：连接EF．弧AB的长是：
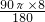=4π（cm）；扇形CAB的面积是：
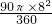=16π（cm2）；等腰直角△CEF的面积是
×8×4=16（cm2）；以CD为直径的半圆的面积是：
×（8÷2）2×π=8π（cm2）；圆O的面积是16π（cm2）；
则16π+16π-2×（16+8π）=（16π-32）（cm2）．
故答案是：4π，（16π-32）．
点评：本题主要考查了扇形面积的计算，正确理解阴影部分的面积=扇形CAB的面积+圆O的面积-2（△CEF的面积+半圆的面积）是解题的关键．
练习册系列答案
相关题目
如图，有一直径是1cm的圆形铁皮，要从中剪出一个最大的圆心角是90°的扇形CAB．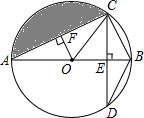
如图，AB为⊙O的直径，CD⊥AB于点E，交⊙O于点D，OF⊥AC于点F．
