题目内容
如图,AB是⊙O的直径,弦BC=2cm,∠B=60°.

(1)求⊙O的半径;
(2)若动点E以2cm/s的速度从A点出发沿着AB方向运动,同时动点F以1cm/s的速度从B点出发沿BC方向运动,设运动时间为t(s)(0<t<2),连结EF,当t为何值时,△BEF为直角三角形?
(3)当t为何值时,△BEF的面积最大?最大面积是多少?

(1)求⊙O的半径;
(2)若动点E以2cm/s的速度从A点出发沿着AB方向运动,同时动点F以1cm/s的速度从B点出发沿BC方向运动,设运动时间为t(s)(0<t<2),连结EF,当t为何值时,△BEF为直角三角形?
(3)当t为何值时,△BEF的面积最大?最大面积是多少?
考点:圆的综合题
专题:
分析:(1)根据圆周角定理可知∠ACB=90°,再由sin∠ABC=
可求出∠B的度数,再根据直角三角形的性质即可求出AB的长进而求出其半径的长;
(2)当△BEF为直角三角形时,与△ABC相似,可根据相似三角形的性质解答;
(3)用含t的代数式表示出△BEF的高,进而用二次函数表示出其面积,利用二次函数的性质解答即可.
| ||
| 2 |
(2)当△BEF为直角三角形时,与△ABC相似,可根据相似三角形的性质解答;
(3)用含t的代数式表示出△BEF的高,进而用二次函数表示出其面积,利用二次函数的性质解答即可.
解答:解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∵sin∠ABC=
,
∴∠ABC=60°,
∴∠A=30°,AB=2BC=4cm,
∴OA=
=
=2cm,即r=2cm;
(2)①当EF⊥BC时,如图1,
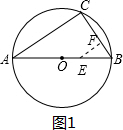
因为AB为⊙O直径,
所以∠C=90°,
当EF⊥BC,
则有△EBF∽△ABC,
于是
=
,
即
=
,
解得t=1.
②当EF⊥AB时,如图2,
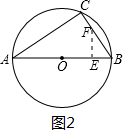
则有△EBF∽△BCA,
于是
=
,
即
=
,
解得t=
.
所以,当t=1s或
s时,△BEF为直角三角形.
(3)作△BFE的BE边上的高FG,如图3,
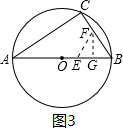
则FG=BF•sin∠ABC=
t.
S△EFB=
EB•FG=
(4-2t)
t=-
t2+
t,
当t=-
=1时,S△EFB取得最大值,为S最大=-
+
=
.
∴∠ACB=90°,
∵sin∠ABC=
| ||
| 2 |
∴∠ABC=60°,
∴∠A=30°,AB=2BC=4cm,
∴OA=
| AB |
| 2 |
| 4 |
| 2 |
(2)①当EF⊥BC时,如图1,

因为AB为⊙O直径,
所以∠C=90°,
当EF⊥BC,
则有△EBF∽△ABC,
于是
| BF |
| BC |
| BE |
| BA |
即
| t |
| 2 |
| 4-2t |
| 4 |
解得t=1.
②当EF⊥AB时,如图2,

则有△EBF∽△BCA,
于是
| EB |
| CB |
| BF |
| AB |
即
| t |
| 4 |
| 4-2t |
| 2 |
解得t=
| 8 |
| 5 |
所以,当t=1s或
| 8 |
| 5 |
(3)作△BFE的BE边上的高FG,如图3,

则FG=BF•sin∠ABC=
| ||
| 2 |
S△EFB=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
当t=-
| ||||
2×(-
|
| ||
| 2 |
| 3 |
| ||
| 2 |
点评:此题是一道综合性很强的题目,涉及圆周角定理、三角函数、二次函数的最值等问题,难度较大,要认真对待.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
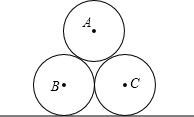 如图,某城市公园的雕塑是焊接固定在水平地面上的3个直径均为2m的两两外切的圆,请求出雕塑的最高点到地面的距离.(提示:构建适当的三角形辅助解答)
如图,某城市公园的雕塑是焊接固定在水平地面上的3个直径均为2m的两两外切的圆,请求出雕塑的最高点到地面的距离.(提示:构建适当的三角形辅助解答) 操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为a、b、c(如图①),分别用4张这样的直角三角形纸片拼成如图②③的形状,图②中的两个小正方形的面积S2、S3与图③中小正方形的面积S1有什么关系?你能得到a、b、c之间有什么关系?
操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为a、b、c(如图①),分别用4张这样的直角三角形纸片拼成如图②③的形状,图②中的两个小正方形的面积S2、S3与图③中小正方形的面积S1有什么关系?你能得到a、b、c之间有什么关系? 如图所示,在边长为a的正方形纸片的一边裁去两个半径为
如图所示,在边长为a的正方形纸片的一边裁去两个半径为