题目内容
9.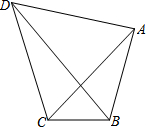 如图,四边形ABCD中,AB=3,BC=2,若AC=AD且∠ACD=60°,则对角线BD的长最大值为5.
如图,四边形ABCD中,AB=3,BC=2,若AC=AD且∠ACD=60°,则对角线BD的长最大值为5.
分析 如图,在AB的右侧作等边三角形△ABK,连接DK.由△DAK≌△CAB,推出DK=BC=2,因为DK+KB≥BD,DK=2,KB=AB=3,所以当D、K、B共线时,BD的值最大,最大值为DK+KB=5.
解答 解:如图,在AB的右侧作等边三角形△ABK,连接DK.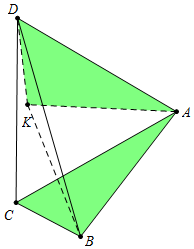
∵AD=AC,AK=AB,∠DAC=∠KAB,
∴∠DAK=∠CAB,
在△DAK和△CAB中,
$\left\{\begin{array}{l}{DA=CA}\\{∠DAK=∠CAB}\\{KA=BA}\end{array}\right.$,
∴△DAK≌△CAB,
∴DK=BC=2,
∵DK+KB≥BD,DK=2,KB=AB=3,
∴当D、K、B共线时,BD的值最大,最大值为DK+KB=5.
故答案为5.
点评 本题考查等边三角形的性质、全等三角形的判定和性质,三角形的三边关系定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,所以中考填空题中的压轴题.

练习册系列答案
相关题目
18.等腰三角形的一个角是100°,则它的顶角的度数是( )
| A. | 100° | B. | 100°或20° | C. | 100°或50° | D. | 20° |
 如图,∠3和∠9是直线AD、BD被直线AC所截而成的同位角;∠6和∠9是直线BC、AC被直线BD所截而成的同位角.
如图,∠3和∠9是直线AD、BD被直线AC所截而成的同位角;∠6和∠9是直线BC、AC被直线BD所截而成的同位角.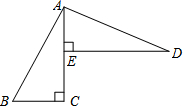 已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.
已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.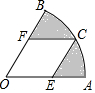 如图,在扇形OAB中,∠O=60°,OA=4$\sqrt{3}$,四边形OECF是扇形OAB中最大的菱形,其中点E,C,F分别在OA,$\widehat{AB}$,OB上,则图中阴影部分的面积为8π-8$\sqrt{3}$.
如图,在扇形OAB中,∠O=60°,OA=4$\sqrt{3}$,四边形OECF是扇形OAB中最大的菱形,其中点E,C,F分别在OA,$\widehat{AB}$,OB上,则图中阴影部分的面积为8π-8$\sqrt{3}$.