Question

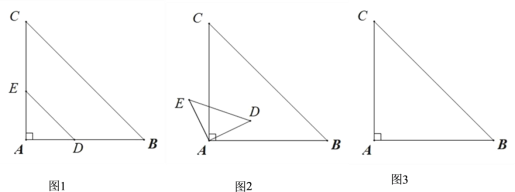
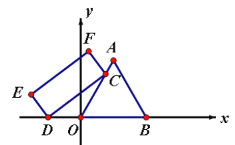
【题目】如图，等边△AOB，点C是边AO所在直线上的动点，点D是x轴上的动点，在矩形CDEF中，CD=6，DE=，则OF的最小值为___________．

Answer 1

【答案】

【解析】

由已知可知∠COD=120°，CD=6，根据定弦定角是圆，找到 △COD的外接圆圆心G位于EF的中点，即可利用点到圆上的距离最小值解决题．

解：取EF的中点G，连接DG、CD、OG，并以DG为半径以G为圆心作圆，

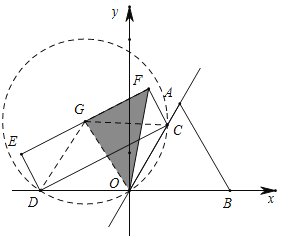
∵在矩形CDEF中，CD=6，DE=，

∴EG=FG=3，

∴tan∠EGD=

∴∠EGD=30°，DG=CG=,

∴∠CGD=120°，

∵在等边△AOB中∠AOB=60°，

∴∠AOD=120°，

∴，

∴C、D、O和圆G上任意一点共圆，即点O在上，

∴DG=OG=，

在△FGO中，，

∴，

∴OF的最小值为．

故答案为：．