题目内容
15.若函数y=$\frac{m}{2}{x}^{2}$+(m+2)x+m+2的图象与x轴只有一个公共点,则m=±2.分析 函数y=$\frac{m}{2}{x}^{2}$+(m+2)x+m+2的图象与x轴只有一个公共点,则△=0,据此即可列方程求解.
解答 解:∵a=$\frac{m}{2}$,b=m+2,c=m+2,
∴b2-4ac=(m+2)2-4×$\frac{m}{2}$×(m+2)=(m+2)2-2m(m+2)=(m+2)(2-m).
则(m+2)(2-m)=0.
解得:m=-2或2.
故答案是:±2.
点评 本题考查了二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点个数与一元二次方程ax2+bx+c=0根之间的关系.△=b2-4ac决定抛物线与x轴的交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;
△=b2-4ac=0时,抛物线与x轴有1个交点;
△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
6.下列运算正确的是( )
| A. | 0-$\frac{1}{2}$=$\frac{1}{2}$ | B. | (-1)+(-$\frac{1}{2}$)=$\frac{3}{2}$ | C. | 2×(-$\frac{1}{2}$)=1 | D. | 2÷(-$\frac{1}{2}$)=-4 |
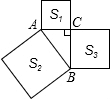 如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积,若S1=9,S2=16,则S3=7.
如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积,若S1=9,S2=16,则S3=7.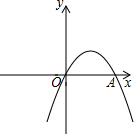 如图,抛物线y=-x2+bx+c经过坐标原点,并与x轴相交于点A(2,0).
如图,抛物线y=-x2+bx+c经过坐标原点,并与x轴相交于点A(2,0). 如图所示,直线AB、CD相交于点O,作∠DOB=∠DOE,OF平分∠AOE,若∠AOC=36°,则∠EOF=54°.
如图所示,直线AB、CD相交于点O,作∠DOB=∠DOE,OF平分∠AOE,若∠AOC=36°,则∠EOF=54°.