题目内容
11.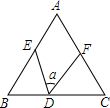 如图,在△ABC中,AB=AC,BE=CD,BD=CF,则∠α与∠A之间的数量关系为2∠α+∠A=180°.
如图,在△ABC中,AB=AC,BE=CD,BD=CF,则∠α与∠A之间的数量关系为2∠α+∠A=180°.
分析 根据SAS证明△BED与△CDF全等,再利用全等三角形的性质解答即可.
解答 解:∵AB=AC,
∴∠C=∠B,
在△BED与△CDF中,
$\left\{\begin{array}{l}{BE=CD}\\{∠B=∠C}\\{BD=CF}\end{array}\right.$,
∴△BED≌△CDF(SAS),
∴∠BED=∠FDC,
∵∠α+∠FDC=∠B+∠BED,
∴∠α=∠B,
∵∠A+∠B+∠C=180°,
∴2∠α+∠A=180°.
故答案为:2∠α+∠A=180°.
点评 本题考查了全等三角形的判定和性质,三角形外角的性质和三角形内角和定理,熟练掌握性质定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,点C是线段AB的黄金分割点,则下列各式正确的是( )
如图,点C是线段AB的黄金分割点,则下列各式正确的是( )
 如图,点C是线段AB的黄金分割点,则下列各式正确的是( )
如图,点C是线段AB的黄金分割点,则下列各式正确的是( )| A. | $\frac{AC}{BC}=\frac{AB}{AC}$ | B. | $\frac{BC}{AB}=\frac{AC}{BC}$ | C. | $\frac{AC}{AB}=\frac{AB}{BC}$ | D. | $\frac{BC}{AB}=\frac{AC}{AB}$ |
3.下列代数式中a,-2ab,x+y,x2+y2,-1,单项式共有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
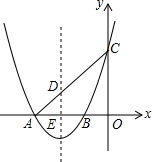 如图,抛物线y=x2+bx+c交x轴于A(-3,0),B(-1,0)两点,交y轴于点C.已知一次函数y=kx+b的图象过点A,C.
如图,抛物线y=x2+bx+c交x轴于A(-3,0),B(-1,0)两点,交y轴于点C.已知一次函数y=kx+b的图象过点A,C. 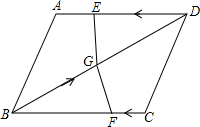 如图,在四边形ABCD中,AD=BC=10,AB=CD,BD=12,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C,作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
如图,在四边形ABCD中,AD=BC=10,AB=CD,BD=12,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C,作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.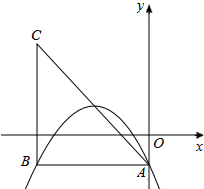 在平面直角坐标系中,已知抛物线y=ax2-2x+c(a,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,-1),C的坐标为(-4,3),直角顶点B在第二象限.
在平面直角坐标系中,已知抛物线y=ax2-2x+c(a,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,-1),C的坐标为(-4,3),直角顶点B在第二象限.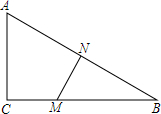 已知△ABC,∠ACB=90°,AC=4,MN垂直平分AB,且BM=2CM,求CM的长.
已知△ABC,∠ACB=90°,AC=4,MN垂直平分AB,且BM=2CM,求CM的长. 如图,已知AB=AC,AB=10cm,CD=3cm,AB的垂直平分线MN交AC于点D,则BD=7cm.
如图,已知AB=AC,AB=10cm,CD=3cm,AB的垂直平分线MN交AC于点D,则BD=7cm.