Question

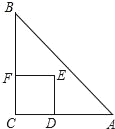
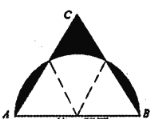
【题目】如图，AB为⊙O的直径，C、D是半圆AB的三等分点，过点C作AD延长线的垂线CE，垂足为E．

（1）求证：CE是⊙O的切线；

（2）若⊙O的半径为2，求图中阴影部分的面积．

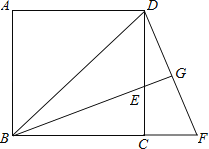
（3）若弦CN过△ABC的内心点M，MN＝，求CN．

Answer 1

【答案】（1）证明见解析；（2） ；（3）CN＝．

【解析】

（1）由已知条件得出，由圆周角定理得出∠BOC=∠A，证出OC∥AD，再由已知条件得出CE⊥OC，即可证出CE为⊙O的切线；

（2）连接OD，OC，由，得到∠COD=×180°=60°，根据CD∥AB，得到S△ACD=S△COD，根据扇形的面积公式即可得到结论．

（3）过点B作BP⊥CN，证明△MCB∽△BCN，得，代入相关数据即可得解.

证明：（1）如图1，连接OD，OC，

∵点C、D为半圆O的三等分点，

∴，

∴∠BOC＝∠BAE，

∴OC∥AD，

∵CE⊥AD，

∴CE⊥OC，

∴CE为⊙O的切线；

（2）∵，

∴∠COD＝×180°＝60°，

∵CD∥AB，

∴S△ACD＝S△COD，

∴图中阴影部分的面积＝S扇形COD＝＝；

（3）如图2，过点B作BP⊥CN，

∵点M是△ACB的内心，

∴∠ACN＝∠BCN＝45°，∠CBM＝∠ABC＝30°，

∵BP⊥CN，

∴∠NCB＝∠CBP＝45°，

∴CP＝BP＝BC，

∵∠CAB＝∠CNB＝30°，

∴PN＝PB＝BC，

∴CN＝PN+CP＝BC，

∵∠CBM＝∠CNB＝30°，∠MCB＝∠NCB，

∴△MCB∽△BCN，

∴，

∴BC2＝BC×（BC﹣2），

∴BC＝2，

∴CN＝×2＝．