题目内容
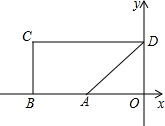 四边形ABCD是直角梯形,∠BAD=135°,∠C=90°,AD=
四边形ABCD是直角梯形,∠BAD=135°,∠C=90°,AD= ,AB=9,求点A、B、C、D的坐标.
,AB=9,求点A、B、C、D的坐标.
解:∵∠BAD=135°,
∴∠DAO=180°-∠BAD=180°-135°=45°,
∵∠AOD=90°,
∴∠ADO=45°,
∴OA=OD=AD•sin45°= ×
× =
= ,
,
∴A(- ,
, ),D(0,
),D(0, ),
),
∵AB=9,
∴OB=AB+OA=9+ ,
,
∴B(-9- ,0),
,0),
∵四边形ABCD是直角梯形,
∴∠C=∠CBA=∠BOD=90°,
∴四边形OBCD是矩形,
∴CD=OB,BC=OD,
∴C(-9- ,
, ).
).
∴A(- ,
, ),B(-9-
),B(-9- ,0),C(-9-
,0),C(-9- ,
, ),D(0,
),D(0, ).
).
分析:由∠BAD=135°,即可得△OAD是等腰直角三角形,又由AD= ,即可求得OA与OD的长,则可求得A与D的坐标,又由AB=9,即可求得点B的坐标,然后由四边形ABCD是直角梯形,易得四边形OBCD是矩形,则可求得点C的坐标.
,即可求得OA与OD的长,则可求得A与D的坐标,又由AB=9,即可求得点B的坐标,然后由四边形ABCD是直角梯形,易得四边形OBCD是矩形,则可求得点C的坐标.
点评:此题考查了直角梯形的性质、矩形的判定与性质、等腰直角三角形的性质以及坐标与图形的性质等知识.此题难度不大,解题的关键是得到△AOD是等腰直角三角形,四边形OBCD是矩形,注意数形结合思想的应用.
∴∠DAO=180°-∠BAD=180°-135°=45°,
∵∠AOD=90°,
∴∠ADO=45°,
∴OA=OD=AD•sin45°=
 ×
× =
= ,
,∴A(-
 ,
, ),D(0,
),D(0, ),
),∵AB=9,
∴OB=AB+OA=9+
 ,
,∴B(-9-
 ,0),
,0),∵四边形ABCD是直角梯形,
∴∠C=∠CBA=∠BOD=90°,
∴四边形OBCD是矩形,
∴CD=OB,BC=OD,
∴C(-9-
 ,
, ).
).∴A(-
 ,
, ),B(-9-
),B(-9- ,0),C(-9-
,0),C(-9- ,
, ),D(0,
),D(0, ).
).分析:由∠BAD=135°,即可得△OAD是等腰直角三角形,又由AD=
 ,即可求得OA与OD的长,则可求得A与D的坐标,又由AB=9,即可求得点B的坐标,然后由四边形ABCD是直角梯形,易得四边形OBCD是矩形,则可求得点C的坐标.
,即可求得OA与OD的长,则可求得A与D的坐标,又由AB=9,即可求得点B的坐标,然后由四边形ABCD是直角梯形,易得四边形OBCD是矩形,则可求得点C的坐标.点评:此题考查了直角梯形的性质、矩形的判定与性质、等腰直角三角形的性质以及坐标与图形的性质等知识.此题难度不大,解题的关键是得到△AOD是等腰直角三角形,四边形OBCD是矩形,注意数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
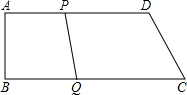
 如图,已知四边形ABCD是直角梯形,AD∥BC,AB⊥BC,四边形ADEF是矩形,其面积为6.28cm2,求阴影部分的面积.
如图,已知四边形ABCD是直角梯形,AD∥BC,AB⊥BC,四边形ADEF是矩形,其面积为6.28cm2,求阴影部分的面积.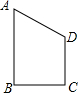 (2013•杭州)四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1,S2,则|S1-S2|=
(2013•杭州)四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1,S2,则|S1-S2|=