题目内容
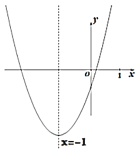
【题目】如图所示,平面直角坐标系中直线![]() 交坐标轴于
交坐标轴于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,点
两点,点![]() 坐标为
坐标为![]() .点
.点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,交抛物线于点
,交抛物线于点![]() .
.

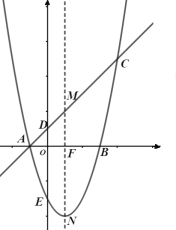
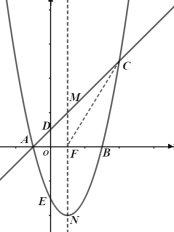
(1)求抛物线的解析式;
(2)是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,如果有,求点
为顶点的四边形为平行四边形,如果有,求点![]() 的坐标,如果没有,请说明理由;
的坐标,如果没有,请说明理由;
(3)若点![]() 在线段
在线段![]() 上移动时(不含端点),连接
上移动时(不含端点),连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)抛物线为![]() ;(2)存在;点M的坐标为(3,4)或(
;(2)存在;点M的坐标为(3,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)当t=
);(3)当t=![]() 时,
时,![]() =
=![]() 为△CMF的面积最大值.
为△CMF的面积最大值.
【解析】
(1)由图形可得出点A、C的坐标,代入抛物线![]() 即可解得;
即可解得;
(2)假设存在,设M(t,t+1),则![]() =t,解得DE=4,以D、E、M、N为顶点的的四边形是平行四边形,结合图形DE∥MN且DE=MN,列出方程式
=t,解得DE=4,以D、E、M、N为顶点的的四边形是平行四边形,结合图形DE∥MN且DE=MN,列出方程式![]() ,求解即可;
,求解即可;
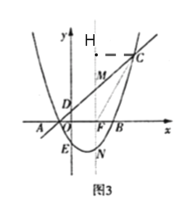
(3)过C作CH⊥MF交FM延长线于H,得到![]() ,代入数据得到关于x的二次函数式,利用最值问题即可得出结果.
,代入数据得到关于x的二次函数式,利用最值问题即可得出结果.
(1)∵直线![]() 过点A,
过点A,
∴点A的坐标为(-1,0),
把点C(![]() ,5)代入直线解析式,
,5)代入直线解析式,
∴![]() =5-1=4,即点C(4,5),
=5-1=4,即点C(4,5),
把点A(-1,0),C(4,5)代入抛物线解析式得
![]() ,
,
解得![]() ,
,
∴抛物线的解析式为:![]() ,
,
故答案为:![]() ;
;
(2)假设存在,设M(t,t+1),则![]() =t,
=t,
∴![]() ,
,
当x=0时,![]() ,点D(0,1)
,点D(0,1)
∴DE=4,
∵DE∥MN,且D、E、M、N为顶点的的四边形是平行四边形,
∴DE=MN,
∴MN=![]() =4,
=4,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解![]() ,得
,得![]() =0(舍)或
=0(舍)或![]() =3;
=3;
解![]() ,得
,得![]() =
=![]() 或
或![]() =
=![]() ,
,
∴综上所述,点M的坐标为(3,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
故答案为:存在;(3,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)同(2)设M(t,t+1),
∵M在线段AC上,
∴-1<t<4,
过C作CH⊥MF交FM延长线于H,
![]() ,
,
=![]() (t+1)(4-t),
(t+1)(4-t),
=![]() ,
,
=![]() ,
,
当t=![]() 时,
时,![]() =
=![]() 为△CMF的面积最大值,
为△CMF的面积最大值,
答:△CMF的面积最大值为![]() ,
,
故答案为:![]() .
.

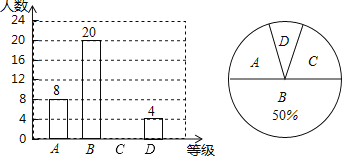
【题目】体育理化考试前夕,九(2)班组织了体育理化考试模拟(体育+理化=100分),模拟测试后相关负责人对成绩进行了统计,制作如下频数分布表和频数分布直方图,请根据表中信息解答问题:
分数段( | 频数 | 频率 |
| 5 | 0.1 |
| 5 |
|
|
| 0.4 |
| 15 | 0.3 |
| 5 | 0.1 |
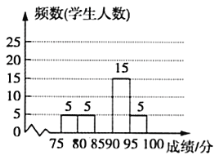
(1)表中![]() ________,
________,![]() ________,并补全直方图;
________,并补全直方图;
(2)若用扇形统计图描述此成绩分布情况,则分数段![]() 所对应扇形的圆心角度数是_____;
所对应扇形的圆心角度数是_____;
(3)若该校九年级共950名学生,请估计该年级分数在![]() 的学生有多少人?
的学生有多少人?