题目内容
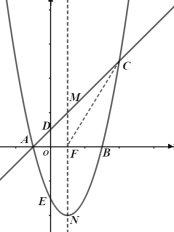
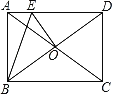
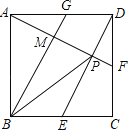
【题目】如图，
为线段
的中点，
与
交于点
，且
交
于
，
交
于
，连
，若
，则
____．
【答案】
【解析】
根据已知条件，∠DME=∠A=∠B=45°，结合三角形外角的性质，即可推出AMF∽△BGM，再根据相似三角形的性质，推出BG的长度，依据锐角三角函数推出AC的长度，即可求出CG、CF的长度，进而推出FG的长度．
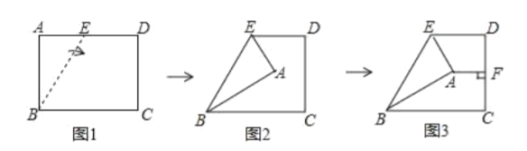
解：∵∠AFM=∠DME+∠E（外角定理），
∠DME=∠A=∠B（已知），
∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG，∠A=∠B，
∴△AMF∽△BGM，
∵∠DME=∠A=∠B=45°
∴AC=BC，∠ACB=90°，
∴AC⊥BC，
∵M为AB的中点，
∴AM=BM=
，
∵△AMF∽△BGM，
∴
，
∴
，
AC=BC=
cos45°=4，
∴CG=4-
=
，CF=4-3=1，
在Rt△FCG中，由勾股定理得：
，
故答案为：
练习册系列答案
相关题目
【题目】“每天锻炼一小时，健康生活一辈子”为了选拔“阳光大课间”领操员，学校组织初中三个年级推选出来的
名领操员进行比赛，成绩如下表：
成绩（分） |
|
|
|
|
人数（人） |
|
|
|
|
（1）这组数据的众数是______，中位数是_______；
（2）已知获得
分的选手中，七、八、九年级分别有
人、
人、人，学校准备从中随机抽取两人领操，求恰好抽到八年级两名领操员的概率．
