题目内容
12.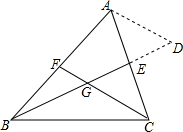 如图,△ABC的中线BE,CF相交于点G,用图中添加辅助线的方法(延长BE到D,GD=BG,连接AD)证明:BG=2GE,CG=2GF.
如图,△ABC的中线BE,CF相交于点G,用图中添加辅助线的方法(延长BE到D,GD=BG,连接AD)证明:BG=2GE,CG=2GF.
分析 根据三角形中位线定理证明AD=2FG,FG∥AD,证明△AED≌△CEG,得到AD=CG,GE=ED,证明结论.
解答 证明:∵GD=BG,BF=FA,
∴FG是△ABD的中位线,
∴AD=2FG,FG∥AD,
∴∠DAE=∠ACF,
在△AED和△CEG中,
$\left\{\begin{array}{l}{∠EAD=∠ECG}\\{AE=EC}\\{∠AED=∠CEG}\end{array}\right.$,
∴△AED≌△CEG,
∴AD=CG,GE=ED,
∴BG=2GE,CG=2GF.
点评 本题考查的是三角形的重心的性质,掌握三角形中位线定理是解题的关键,注意全等三角形的判定和性质的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,甲楼每层高都是3.1米,乙楼高40米,从甲楼的第6层往外看乙楼楼顶,仰角为30°,两楼相距AB有多少米?(结果精确到0.1米)
如图,甲楼每层高都是3.1米,乙楼高40米,从甲楼的第6层往外看乙楼楼顶,仰角为30°,两楼相距AB有多少米?(结果精确到0.1米) 已知一次函数y=kx+b的图象如图,当x<0时,y的取值范围是y>2.
已知一次函数y=kx+b的图象如图,当x<0时,y的取值范围是y>2. 如图,锐角三角形ABC内接于⊙O,BC=$\sqrt{3}$,AC=$\sqrt{2}$,∠A=60°,求⊙O的半径R及∠B,∠C.
如图,锐角三角形ABC内接于⊙O,BC=$\sqrt{3}$,AC=$\sqrt{2}$,∠A=60°,求⊙O的半径R及∠B,∠C.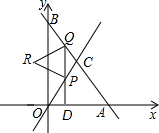 已知在平面直角坐标系中,直线y=-$\sqrt{3}$x+6$\sqrt{3}$与x轴,y轴相交于A、B两点,直线y=$\sqrt{3}$x与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运动到点A,过点D作x轴的垂线,分别交直线y=$\sqrt{3}$x和直线y=-$\sqrt{3}$x+6$\sqrt{3}$于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设点D的运动时间为t(秒)
已知在平面直角坐标系中,直线y=-$\sqrt{3}$x+6$\sqrt{3}$与x轴,y轴相交于A、B两点,直线y=$\sqrt{3}$x与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运动到点A,过点D作x轴的垂线,分别交直线y=$\sqrt{3}$x和直线y=-$\sqrt{3}$x+6$\sqrt{3}$于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设点D的运动时间为t(秒)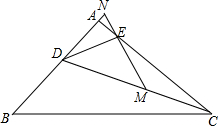 已知:在Rt△ABC中,∠BAC=90°,CD平分∠ACB,∠EDC=45°,过点E作DE的垂线,交DC于M,交BA延长线于N.若NE:MC=$\sqrt{2}$:3,BD=5,则BC=10.
已知:在Rt△ABC中,∠BAC=90°,CD平分∠ACB,∠EDC=45°,过点E作DE的垂线,交DC于M,交BA延长线于N.若NE:MC=$\sqrt{2}$:3,BD=5,则BC=10.