题目内容
2.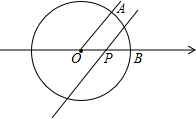 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若点P对应的实数为x,过点P且与OA平行的直线与⊙O没有公共点,则x的取值范围是-$\sqrt{2}$≤x≤$\sqrt{2}$且x≠0.
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若点P对应的实数为x,过点P且与OA平行的直线与⊙O没有公共点,则x的取值范围是-$\sqrt{2}$≤x≤$\sqrt{2}$且x≠0.
分析 由题意得x有两个极值点,过点P与⊙O相切时,x取得极值,作出切线,利用切线的性质求解即可.
解答 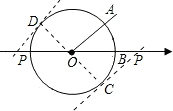 解:将OA平移至P'D的位置,使P'D与圆相切,
解:将OA平移至P'D的位置,使P'D与圆相切,
连接OD,由题意得,OD=1,∠DOP'=45°,∠ODP'=90°,
故可得OP'=$\sqrt{2}$,即x的极大值为$\sqrt{2}$,
同理当点P在y轴左边时也有一个极值点,此时x取得极小值,x=-$\sqrt{2}$,
综上可得x的范围为:-$\sqrt{2}$≤x≤$\sqrt{2}$.
又∵DP'与OA平行,
∴x≠0,
故答案为:-$\sqrt{2}$≤x≤$\sqrt{2}$且x≠0.
点评 此题主要考查了直线与圆的位置关系,分别得出两圆与圆相切时求出OP的长是解决问题的关键,难度一般,注意两个极值点的寻找.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,CD⊥AB,垂足为点D,以点C为圆心,3为半径画圆,则A、B、D三点中在圆外的是B,在圆内的是D,在圆上的是A.
如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,CD⊥AB,垂足为点D,以点C为圆心,3为半径画圆,则A、B、D三点中在圆外的是B,在圆内的是D,在圆上的是A. 如图,已知⊙O的半径为5,弦AB=6,则⊙O上到弦AB所在直线的距离等于2的点有2个.
如图,已知⊙O的半径为5,弦AB=6,则⊙O上到弦AB所在直线的距离等于2的点有2个. 如图所示,用四段木条做一个平行四边形的活动木框ABCD,将其水平放置在桌面上,轻轻地推动点D,可以发现形状改变了,但不管如何(只要A,B,C,D不共线),它仍然保持平行四边形的形状;当∠D恰为直角(即90°)时,就得到一个特殊的平行四边形,即矩形.
如图所示,用四段木条做一个平行四边形的活动木框ABCD,将其水平放置在桌面上,轻轻地推动点D,可以发现形状改变了,但不管如何(只要A,B,C,D不共线),它仍然保持平行四边形的形状;当∠D恰为直角(即90°)时,就得到一个特殊的平行四边形,即矩形. 如图,两个正方形ABDE和ACFG如图摆放.
如图,两个正方形ABDE和ACFG如图摆放.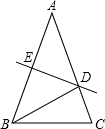 如图所示,△ABC中,AB=AC=14cm,BC=10cm,AB的垂直平分线交AC于D,垂足为E,则△BCD的周长是24cm.
如图所示,△ABC中,AB=AC=14cm,BC=10cm,AB的垂直平分线交AC于D,垂足为E,则△BCD的周长是24cm.