题目内容
如图在矩形ABCD中,AB=1,AD=2,现将一块直径为2的半圆形纸片放置在矩形ABCD中,使其直径与AD重合,若将半圆上点D 固定,再把半圆往矩形外旋至A′D处,半圆弧A′D与AD交于点P, 设∠ADA′ =α,

(1)若AP =2- ,求α的度数;
,求α的度数;
(2)当∠α =30° 时,求阴影部分的面积。
 ,求α的度数;
,求α的度数;(2)当∠α =30° 时,求阴影部分的面积。
解:(1)连接PA则∠A′PD=90°
∵AD=A′D=2且AP=2-
∴PD=
∴cosα= =
=
∴∠а=45°;
(2)连接OP
S阴影面积=S半圆-S弓形PD
=
 -(S扇形POD-
-(S扇形POD- )
)
=
 -
-
= +
+ 。
。
∵AD=A′D=2且AP=2-

∴PD=

∴cosα=
 =
=
∴∠а=45°;
(2)连接OP
S阴影面积=S半圆-S弓形PD
=

 -(S扇形POD-
-(S扇形POD- )
)=

 -
-
=
 +
+ 。
。
练习册系列答案
相关题目
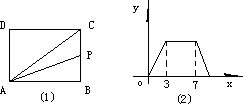
 已知:如图在矩形ABCD中,点E为CD的中点,连接EA、EB. 求证:∠EAB=∠EBA.
已知:如图在矩形ABCD中,点E为CD的中点,连接EA、EB. 求证:∠EAB=∠EBA.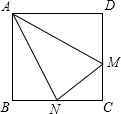 如图在矩形ABCD中,M为CD上一点,沿AM折叠,使D点落在BC上的N点处,如果AD=7cm,DM=5cm,∠DAM=30°,则AN=
如图在矩形ABCD中,M为CD上一点,沿AM折叠,使D点落在BC上的N点处,如果AD=7cm,DM=5cm,∠DAM=30°,则AN=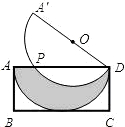 如图在矩形ABCD中,AB=1,AD=2,现将一块直径为2的半圆形纸片放置在矩形ABCD中,使其直径与AD重合,若将半圆上点D固定,再把半圆往矩形外旋至A′D处,半圆弧A′D与AD交于点P,设∠ADA′=α.
如图在矩形ABCD中,AB=1,AD=2,现将一块直径为2的半圆形纸片放置在矩形ABCD中,使其直径与AD重合,若将半圆上点D固定,再把半圆往矩形外旋至A′D处,半圆弧A′D与AD交于点P,设∠ADA′=α.
 ,BC=
,BC= ,当
,当