题目内容
直线![]() 分别交x轴、y轴于A、B两点,△AOB绕点O按逆时针方向旋转90°后得到△COD,抛物线y=ax2+bx+c经过A、C、D三点.
分别交x轴、y轴于A、B两点,△AOB绕点O按逆时针方向旋转90°后得到△COD,抛物线y=ax2+bx+c经过A、C、D三点.
(1) 写出点A、B、C、D的坐标;
(2) 求经过A、C、D三点的抛物线表达式,并求抛物线顶点G的坐标;
(3) 在直线BG上是否存在点Q,使得以点A、B、Q为顶点的三角形与△COD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.

图1
(1)A(3,0),B(0,1),C(0,3),D(-1,0).
(2)因为抛物线y=ax2+bx+c经过A(3,0)、C(0,3)、D(-1,0) 三点,
所以 解得
解得
所以抛物线的解析式为y=-x2+2x+3=-(x-1)2+4,顶点G的坐标为(1,4).
(3)如图2,直线BG的解析式为y=3x+1,直线CD的解析式为y=3x+3,因此CD//BG.
因为图形在旋转过程中,对应线段的夹角等于旋转角,所以AB⊥CD.因此AB⊥BG,即∠ABQ=90°.
因为点Q在直线BG上,设点Q的坐标为(x,3x+1),那么![]() .
.
Rt△COD的两条直角边的比为1∶3,如果Rt△ABQ与Rt△COD相似,存在两种情况:
①当![]() 时,
时,![]() .解得
.解得![]() .所以
.所以![]() ,
,![]() .
.
②当![]() 时,
时,![]() .解得
.解得![]() .所以
.所以![]() ,
,![]() .
.

图2 图3

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•拱墅区一模)如图,在平面直角坐标系中,直线y=-x+1分别交x轴、y轴于A,B两点,点P(a,b)是反比例函数y=
(2012•拱墅区一模)如图,在平面直角坐标系中,直线y=-x+1分别交x轴、y轴于A,B两点,点P(a,b)是反比例函数y=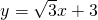 分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
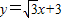 分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
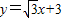 分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.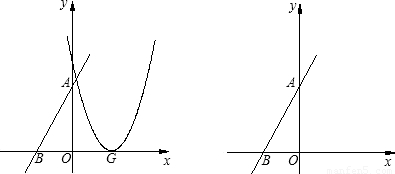
 的两个根,点C在x轴负半轴上,
的两个根,点C在x轴负半轴上,