��Ŀ����
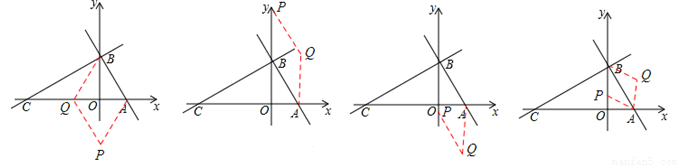
��ͼ��ƽ��ֱ������ϵ�У�ֱ��l�ֱ�x�ᡢy����A��B���㣨OA��OB����OA��OB�ij��ֱ���һԪ���η��� ������������C��x�Ḻ�����ϣ�
������������C��x�Ḻ�����ϣ�
��AB��AC=1��2

��1����A��C��������ꣻ
��2������M��C���������ÿ��1����λ���ٶ�������CB�˶�������AM�����ABM�����ΪS����M���˶�ʱ��Ϊt��д��S����t�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��3����P��y���ϵĵ㣬������ƽ�����Ƿ���ڵ�Q��ʹ�� A��B��P��QΪ������ı��������Σ������ڣ���ֱ��д��Q������ꣻ�������ڣ���˵�����ɣ�
�⣺��1����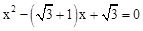 �ã�x��
�ã�x��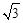 ����x��1��=0��
����x��1��=0��
���x1=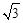 ��x2=1��
��x2=1��
��OA��OB����OA=1��OB=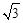 ����A��1��0����B��0��
����A��1��0����B��0��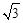 ������AB=2��
������AB=2��
�֡�AB��AC=1��2����AC=4����C����3��0������
��2��������ã�CM=t��CB=2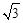 ��
��
�ٵ���M��CB����ʱ��S=2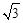 ��t��0��t��
��t��0��t��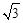 ����
����
�ڵ���M��CB�ߵ��ӳ�����ʱ��S=t��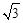 ��t��
��t��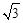 ����
����
��3�����ڣ�Q1����1��0����Q2��1����2����Q3��1��2����Q1��1��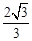 ����
����
��������
�����������1��ͨ����һԪ���η���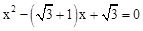 ����÷��̵����������Ӷ��õ�A��B��������꣬�ٸ��ݹ��ɶ�������AB�ij�������AB��AC=1��2������AC�ij����Ӷ��õ�C������ꡣ
����÷��̵����������Ӷ��õ�A��B��������꣬�ٸ��ݹ��ɶ�������AB�ij�������AB��AC=1��2������AC�ij����Ӷ��õ�C������ꡣ
��2���֢ٵ���M��CB����ʱ���ڵ���M��CB�ߵ��ӳ�����ʱ������������ۿ���S����t�ĺ�����ϵʽ��
��3����AB�DZߺͶԽ�������������ۿ���Q������꣺

 ��ͼ��ƽ��ֱ������ϵ�У�OΪֱ��������ABC��ֱ�Ƕ��㣬��B=30�㣬��Ƕ���A��˫����
��ͼ��ƽ��ֱ������ϵ�У�OΪֱ��������ABC��ֱ�Ƕ��㣬��B=30�㣬��Ƕ���A��˫���� =2
=2 ��ͼ��ƽ��ֱ������ϵ�У�OB��x���ϣ���ABO=90�㣬��A������Ϊ��1��2��������AOB�Ƶ�A��ʱ����ת90�㣬���O�Ķ�Ӧ��C������Ϊ��������
��ͼ��ƽ��ֱ������ϵ�У�OB��x���ϣ���ABO=90�㣬��A������Ϊ��1��2��������AOB�Ƶ�A��ʱ����ת90�㣬���O�Ķ�Ӧ��C������Ϊ��������
 ��ͼ��ƽ��ֱ������ϵ�У�A������Ϊ��8��0����B������Ϊ��0��6��C���߶�AB���е㣮������y�����Ƿ����һ��P��ʹ����P��B��CΪ��������������AOB���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
��ͼ��ƽ��ֱ������ϵ�У�A������Ϊ��8��0����B������Ϊ��0��6��C���߶�AB���е㣮������y�����Ƿ����һ��P��ʹ����P��B��CΪ��������������AOB���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�