题目内容
5.计算:(1)3$\sqrt{18}$+$\frac{\sqrt{50}}{5}$-4$\sqrt{0.5}$;
(2)$\sqrt{27}$-15$\sqrt{\frac{1}{3}}$+$\frac{1}{4}$$\sqrt{48}$;
(3)$\sqrt{6}$-$\sqrt{\frac{3}{2}}$-$\sqrt{\frac{2}{3}}$+$\sqrt{48}$-$\sqrt{12}$.
分析 对题目中的式子先化简,再合并同类项,即可得到问题的答案.
解答 解:(1)3$\sqrt{18}$+$\frac{\sqrt{50}}{5}$-4$\sqrt{0.5}$
=$9\sqrt{2}+\frac{5\sqrt{2}}{5}-4×\frac{\sqrt{2}}{2}$
=$9\sqrt{2}+\sqrt{2}-2\sqrt{2}$
=$8\sqrt{2}$;
(2)$\sqrt{27}$-15$\sqrt{\frac{1}{3}}$+$\frac{1}{4}$$\sqrt{48}$
=$3\sqrt{3}-15×\frac{\sqrt{3}}{3}+\frac{1}{4}×4\sqrt{3}$
=$3\sqrt{3}-5\sqrt{3}+\sqrt{3}$
=-$\sqrt{3}$;
(3)$\sqrt{6}$-$\sqrt{\frac{3}{2}}$-$\sqrt{\frac{2}{3}}$+$\sqrt{48}$-$\sqrt{12}$
=$\sqrt{6}-\frac{\sqrt{6}}{2}-\frac{\sqrt{6}}{3}+4\sqrt{3}-2\sqrt{3}$
=$\frac{\sqrt{6}}{6}+2\sqrt{3}$.
点评 本题考查二次根式的加减法,解题的关键是将二次根式要化到最简.

练习册系列答案
相关题目
3.下列各组长度线段能组成三角形的是( )
| A. | 1cm,3cm,5cm | B. | 1cm,1cm,2cm | C. | 1cm,2cm,3cm | D. | 1cm,2cm,2cm |
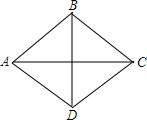 如图,菱形ABCD的边长为10,sin∠BAC=$\frac{3}{5}$,则对角线AC的长为16.
如图,菱形ABCD的边长为10,sin∠BAC=$\frac{3}{5}$,则对角线AC的长为16.
 ,其中
,其中 .
.